题目内容
2. 如图所示是回旋加速器的示意图,其核心部分是两个D形金属盒,在加速带电粒子时,两金属盒置于磁感应强度大小为B的匀强磁场中,并分别与高频电源相连,已知加速电压为U,D形金属盒的半径为R,两盒之间狭缝距离为d.若在D形盒中心处粒子源产生质量为m,电荷量为+q的质子在加速器中被加速,(忽略粒子质量变化,忽略粒子重力)则下列判断中正确的是( )
如图所示是回旋加速器的示意图,其核心部分是两个D形金属盒,在加速带电粒子时,两金属盒置于磁感应强度大小为B的匀强磁场中,并分别与高频电源相连,已知加速电压为U,D形金属盒的半径为R,两盒之间狭缝距离为d.若在D形盒中心处粒子源产生质量为m,电荷量为+q的质子在加速器中被加速,(忽略粒子质量变化,忽略粒子重力)则下列判断中正确的是( )| A. | 质子获得最大速度$\frac{{q}^{2}{R}^{2}{B}^{2}}{m}$ | |
| B. | 质子每次加速经过D形盒间的狭缝轨道半径是加速前轨道半径的2倍 | |
| C. | 质子在电场中与磁场中运动总时间为t=$\frac{πB{R}^{2}}{2U}$+$\frac{BRd}{U}$ | |
| D. | 不改变磁感应强度B和交变电流的频率f,该回旋加速器也能用于加速氘核 |
分析 根据动能定理,结合D形金属盒的半径为R,即可求解加速的最大动能;由洛伦兹力提供向心力,结合周期公式,即可求得加速器的回转频率的关系式,从而即可求解.
解答 解:A、由qvmB=$\frac{m{v}_{m}^{2}}{R}$ 得R=$\frac{m{v}_{m}}{qB}$
那么vm=$\frac{BqR}{m}$,粒子获得的最大动能Ekm=$\frac{{q}^{2}{B}^{2}{R}^{2}}{2m}$,故A错误;
B、由动能定理可得△Ek=qU,可知每次加速动能增加相同,但速度增加不是相同,根据R=$\frac{mv}{Bq}$,可知,狭缝轨道半径不是加速前轨道半径的2倍,故B错误;
C、设粒子加速的次数为N,由动能定理可得:NqU=Ekm=$\frac{{q}^{2}{B}^{2}{R}^{2}}{2m}$,
则有:N=$\frac{q{B}^{2}{R}^{2}}{2mU}$,故在磁场中运动的时间为:tB=$\frac{N}{2}$T=$\frac{πB{R}^{2}}{2U}$,
在电场中匀加速运动:Nd=$\frac{1}{2}$$\frac{qU}{md}$tE2
解得:tE=d$\sqrt{\frac{2mN}{qU}}$,
故在电磁场中运动的总时间为:t=$\frac{πB{R}^{2}}{2U}$+d$\sqrt{\frac{2mN}{qU}}$=$\frac{πB{R}^{2}}{2U}$+$\frac{BRd}{U}$,故C正确;
D、加速粒子的周期等于交变电流的周期,故不改变磁感应强度B和交变电流的频率f,该回旋加速度器不能用于加速氘核,故D错误;
故选:C.
点评 考查粒子在电场中加速与在磁场偏转,掌握动能定理与牛顿第二定律及向心力表达式的综合应用,注意加速度的最大动能与加速电压无关,而加速的回转频率与粒子的比荷有关,是解题的关键.

 在光滑的绝缘水平面上,有一个正方形的abcd,顶点a、c处分别固定一个电荷量相等的正点电荷,如图所示.若将一个带负电的粒子置于b点,自由释放,粒子将沿着对角线bd往复运动.粒子从b点运动到d点的过程中( )
在光滑的绝缘水平面上,有一个正方形的abcd,顶点a、c处分别固定一个电荷量相等的正点电荷,如图所示.若将一个带负电的粒子置于b点,自由释放,粒子将沿着对角线bd往复运动.粒子从b点运动到d点的过程中( )| A. | 先作匀加速运动,后作匀减速运动,在中点o速度最大 | |
| B. | 先从高电势到低电势,后从低电势到高电势 | |
| C. | 从b到o过程,电势能从最大减小到0,动能从o增大到最大,机械能守恒 | |
| D. | 从b经o到d过程,电势能先减小后增大,动能先增大后减小,总能量守恒 |
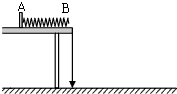 如图所示,将轻弹簧放在光滑的水平轨道上,一端与轨道的A端固定,另一端正好在轨道的B端处,轨道固定在水平桌面的边缘上,桌边悬一重锤.根据平抛运动的规律和功能关系的相关知识,可利用该装置找出弹簧压缩时具有的弹性势能与压缩量之间的关系.
如图所示,将轻弹簧放在光滑的水平轨道上,一端与轨道的A端固定,另一端正好在轨道的B端处,轨道固定在水平桌面的边缘上,桌边悬一重锤.根据平抛运动的规律和功能关系的相关知识,可利用该装置找出弹簧压缩时具有的弹性势能与压缩量之间的关系.(1)为完成实验,还需下面哪些器材BD
A.秒表 B.刻度尺 C弹簧秤 D.白纸和复写纸 E.天平
(2)如果在实验中,得到弹簧压缩量x和小球离开桌面后的水平位移s的一些数据如下表,经你的推导分析,得到两者的关系为:弹簧的弹性势能与弹簧压缩量的平方成正比.
| 实验次数 | 1 | 2 | 3 | 4 |
| x/cm | 2.00 | 3.00 | 4.00 | 5.00 |
| s/cm | 10.03 | 15.04 | 20.02 | 25.00 |
| A. | 物体是竖直下落的,其位移大小等于飞机的高度 | |
| B. | 物体是沿曲线下落的,其位移大小小于路程 | |
| C. | 物体是沿曲线下落的,其位移大小等于路程 | |
| D. | 物体是沿曲线下落的,其位移大小等于飞机的高度 |
 一雨滴从屋檐由静止自由下落,通过高度为h=1.8m的窗户时间为t=0.2s,求屋檐到窗台的高度H(g取10m/s2)
一雨滴从屋檐由静止自由下落,通过高度为h=1.8m的窗户时间为t=0.2s,求屋檐到窗台的高度H(g取10m/s2) 如图所示,在真空中相距为L的A、B两点分别放置在同一水平线上,电量大小均为Q的正负点电荷,那么在离A、B两点距离都等于L的点的电场强度方向为由A指向B,该点的场强大小为$k\frac{Q}{{l}^{2}}$.?
如图所示,在真空中相距为L的A、B两点分别放置在同一水平线上,电量大小均为Q的正负点电荷,那么在离A、B两点距离都等于L的点的电场强度方向为由A指向B,该点的场强大小为$k\frac{Q}{{l}^{2}}$.?