题目内容
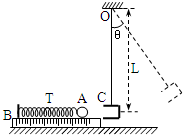 某同学准备利用如图所示的装置探究劲度系数较大的轻质弹簧T的弹性势能与其压缩量之间的关系.图中B为一固定在桌面、带有刻度的平直光滑导轨,小盒C用轻绳悬挂于O点,弹簧T左端固定,用小球A沿导轨B向左挤压弹簧,释放后球A弹出,射入一较重的小盒C中与小盒C一起向右摆动,摆动的最大角度θ可以被准确测出.球A射入盒C后两者的重心重合,重心距悬点O的距离为L.试问:
某同学准备利用如图所示的装置探究劲度系数较大的轻质弹簧T的弹性势能与其压缩量之间的关系.图中B为一固定在桌面、带有刻度的平直光滑导轨,小盒C用轻绳悬挂于O点,弹簧T左端固定,用小球A沿导轨B向左挤压弹簧,释放后球A弹出,射入一较重的小盒C中与小盒C一起向右摆动,摆动的最大角度θ可以被准确测出.球A射入盒C后两者的重心重合,重心距悬点O的距离为L.试问:(1)欲完成此探究实验,该同学在实验过程中除了要测量最大摆角θ和重心距悬点O的距离L外,还需要测量哪些物理量?写出这些物理量及其字母代号.
(2)通过上述的物理量可求出弹簧T将球A弹出时释放的弹性势能EP.写出其计算表达式(无需书写推导过程).
(3)下面是本实验中的几个步骤:①按实验装置安装好器材;②用刻度尺测定C的重心到悬点O的距离L; ③反复调节盒C的位置,使其运动轨迹平面与光滑轨道在同一平面内,且盒C静挂,开口正对导轨末端,A、C两者重心同高;④用球A压缩弹簧,使其重心处于轨道的某一刻度线上,记录此时的读数;⑤释放A球,让它射入盒C中,一起与C摆动到最大高度;⑥记录最大摆角θ;⑦处理数据,得出结论.在上述步骤中还缺少哪些主要步骤?请你写出来.
(4)该实验除了要保证光滑导轨水平、小球A能正射入小盒C并与C一起运动以外,还应注意些什么?
分析:(1)弹簧的弹性势能转化为球和盒子的重力势能,故需要测量球和盒子的质量以及弹簧的压缩量;
(2)弹性势能的减小量等于小球的动能的增加量,碰撞过程动量守恒;向上摆动过程机械能守恒;
(3)对照表达式确定实验步骤;
(4)从实验误差角度考虑,摆角不宜过大,也不宜过小.
(2)弹性势能的减小量等于小球的动能的增加量,碰撞过程动量守恒;向上摆动过程机械能守恒;
(3)对照表达式确定实验步骤;
(4)从实验误差角度考虑,摆角不宜过大,也不宜过小.
解答:解:(1)弹簧的弹性势能转化为球和盒子的重力势能,要测量重力势能的增加量,要测量小球A的质量m、重盒C的质量M;
要研究弹性势能和压缩量的关系,要测量弹簧的压缩量X;
还需测量:小球A的质量m、重盒C的质量M、弹簧的压缩量X;
(2)弹性势能的减小量等于小球的动能的增加量,故Ep=
mv2;
碰撞过程动量守恒,故mv=(M+m)v′
继续摆动过程机械能守恒,故:
(M+m)v′2=(M+m)gL(1-cosθ)
联立解得Ep=
;
(3)缺少的主要实验步骤有:
①用天平称出小球质量和重盒的质量;
②用球A接触弹簧但不压缩,记录其重心位置,读取导轨上相应的读数;
③改变弹簧压缩量,重复实验若干次.
(4)①要注意每次实验时,弹簧压缩量不要过大,以保证绳总处于绷直状态,同时摆角不大于90°;
②每次实验时,弹簧的压缩量也不宜过小,否则压缩量L及摆角θ的测量相对误差大,轨道摩擦损耗不可忽略.
故答案为:(1)小球A的质量m、重盒C的质量M、弹簧的压缩量X;
(2)Ep=
;
(3)缺少的主要实验步骤有:①用天平称出小球质量和重盒的质量;②用球A接触弹簧但不压缩,记录其重心位置,读取导轨上相应的读数; ③改变弹簧压缩量,重复实验若干次.
(4)①要注意每次实验时,弹簧压缩量不要过大,以保证绳总处于绷直状态,同时摆角不大于90°;②每次实验时,弹簧的压缩量也不宜过小,否则压缩量L及摆角θ的测量相对误差大,轨道摩擦损耗不可忽略.
要研究弹性势能和压缩量的关系,要测量弹簧的压缩量X;
还需测量:小球A的质量m、重盒C的质量M、弹簧的压缩量X;
(2)弹性势能的减小量等于小球的动能的增加量,故Ep=
| 1 |
| 2 |
碰撞过程动量守恒,故mv=(M+m)v′
继续摆动过程机械能守恒,故:
| 1 |
| 2 |
联立解得Ep=
| =(M+m)2gL(1-cosθ) |
| m |
(3)缺少的主要实验步骤有:
①用天平称出小球质量和重盒的质量;
②用球A接触弹簧但不压缩,记录其重心位置,读取导轨上相应的读数;
③改变弹簧压缩量,重复实验若干次.
(4)①要注意每次实验时,弹簧压缩量不要过大,以保证绳总处于绷直状态,同时摆角不大于90°;
②每次实验时,弹簧的压缩量也不宜过小,否则压缩量L及摆角θ的测量相对误差大,轨道摩擦损耗不可忽略.
故答案为:(1)小球A的质量m、重盒C的质量M、弹簧的压缩量X;
(2)Ep=
| =(M+m)2gL(1-cosθ) |
| m |
(3)缺少的主要实验步骤有:①用天平称出小球质量和重盒的质量;②用球A接触弹簧但不压缩,记录其重心位置,读取导轨上相应的读数; ③改变弹簧压缩量,重复实验若干次.
(4)①要注意每次实验时,弹簧压缩量不要过大,以保证绳总处于绷直状态,同时摆角不大于90°;②每次实验时,弹簧的压缩量也不宜过小,否则压缩量L及摆角θ的测量相对误差大,轨道摩擦损耗不可忽略.
点评:本题关键明确实验原理、误差来源、实际操作,能运用机械能守恒定律和动量守恒定律列式求解,较难.

练习册系列答案
相关题目
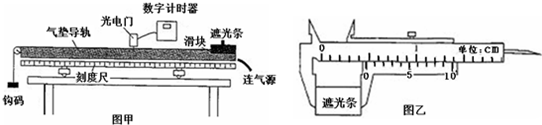
 Ⅰ.某同学在做测定木块与木板间动摩擦因数的实验过程中,测滑动摩擦力时,他设计了两种实验方案.
Ⅰ.某同学在做测定木块与木板间动摩擦因数的实验过程中,测滑动摩擦力时,他设计了两种实验方案.
 某同学准备利用如图所示的装置探究劲度系数较大的轻质弹簧T的弹性势能与其压缩量之间的关系.图中B为一固定在桌面、带有刻度的平直光滑导轨,小盒C用轻绳悬挂于O点,弹簧T左端固定,用小球A沿导轨B向左挤压弹簧,释放后球A弹出,射入一较重的小盒C中与小盒C一起向右摆动,摆动的最大角度θ可以被准确测出.球A射入盒C后两者的重心重合,重心距悬点O的距离为L.试问:
某同学准备利用如图所示的装置探究劲度系数较大的轻质弹簧T的弹性势能与其压缩量之间的关系.图中B为一固定在桌面、带有刻度的平直光滑导轨,小盒C用轻绳悬挂于O点,弹簧T左端固定,用小球A沿导轨B向左挤压弹簧,释放后球A弹出,射入一较重的小盒C中与小盒C一起向右摆动,摆动的最大角度θ可以被准确测出.球A射入盒C后两者的重心重合,重心距悬点O的距离为L.试问:
