Question

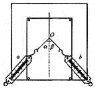
【题目】如图所示，质量为M的平板车P高h，质量为m的小物块Q的大小不计，位于平板车的左端，系统原来静止在光滑水平地面上。一不可伸长的轻质细绳长为R，一端悬于Q正上方高为R处，另一端系一质量也为m的小球（大小不计）。今将小球拉至悬线与竖直位置成60°角，由静止释放，小球到达最低点时与Q的碰撞时间极短，且无能量损失。已知Q离开平板车时速度大小是平板车速度的两倍，Q与P之间的动摩擦因数为μ，M＝4m，重力加速度为g。求：

(1)求小球刚到达最低点的速度大小和碰撞后小物块Q的速度vQ大小；

(2)小物块Q在平板车上运动的时间t；

(3)平板车P的长度L。

Answer 1

【答案】(1) ；vQ＝；(2)；(3)L＝

【解析】

(1)小球由静止摆到最低点的过程中，根据机械能守恒

解得

小球与物块Q相撞时，动量守恒，机械能守恒，则有

mv0＝mv1＋mvQ

解得

v1＝0，

(2)碰后，小球静止下来，Q在平板车上滑行的过程中系统的动量守恒，则有

mvQ＝Mv＋m(2v)

解得

物块Q在板上滑行过程中，由动量定理可得

解得，小物块Q在长木板P上运动时间为

(3)设平板车长L，由能的转化和守恒定律知

解得平板车P的长度为