题目内容
如图所示，能承受最大拉力为10 N的细线OA与竖直方向成45°角，能承受最大拉力为5 N的细线OB水平，细线OC能承受足够的拉力，为使OA、OB均不被拉断，OC下端所悬挂物体的最大重力是多少？
5 N
当OC下端所悬物重不断增大时，细线OA、OB所受的拉力同时增大．为了判断哪根细线先被
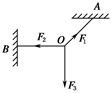
拉断，可选O点为研究对象，其受力情况如图7所示，利用假设，分别假设OA、OB达最大值时，看另一细线是否达到最大值，从而得到结果．取O点为研究对象，受力分析如图7所示，假设OB不会被拉断，且OA上的拉力先达到最大值，即F1＝10 N，根据平衡条件有F2＝F1maxcos45°＝10×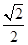
N＝7.07 N，由于F2大于OB能承受的最大拉力，所以在物重逐渐增大时，细线OB先被拉断．
再假设OB线上的拉力刚好达到最大值(即F2max＝5 N)处于将被拉断的临界状态，根据平衡条件有F1·cos45°＝F2max，F1sin45°＝F3.
再选重物为研究对象，根据平衡条件有F3＝Gmax.
以上三式联立解得悬挂最大重物为
Gmax＝F2max＝5 N.
拉断，可选O点为研究对象，其受力情况如图7所示，利用假设，分别假设OA、OB达最大值时，看另一细线是否达到最大值，从而得到结果．取O点为研究对象，受力分析如图7所示，假设OB不会被拉断，且OA上的拉力先达到最大值，即F1＝10 N，根据平衡条件有F2＝F1maxcos45°＝10×
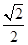N＝7.07 N，由于F2大于OB能承受的最大拉力，所以在物重逐渐增大时，细线OB先被拉断．再假设OB线上的拉力刚好达到最大值(即F2max＝5 N)处于将被拉断的临界状态，根据平衡条件有F1·cos45°＝F2max，F1sin45°＝F3.
再选重物为研究对象，根据平衡条件有F3＝Gmax.
以上三式联立解得悬挂最大重物为
Gmax＝F2max＝5 N.
练习册系列答案
相关题目
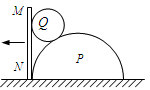
cm时，AB段绳上的拉力为多少.
mg(g表示重力加速度），则轻杆对小球的弹力大小为（ ）
B．
D．