Question

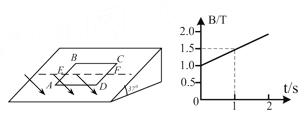
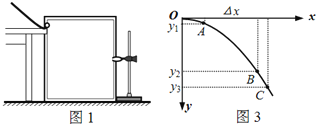
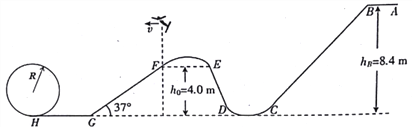
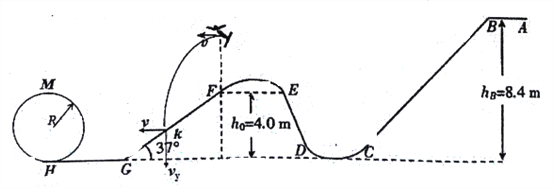
【题目】如图所示为一自由式滑雪空中技巧比赛场地示意图，比赛场地由出发区AB、助滑坡BC、第一过渡区CD、跳台DE、第二过渡区EF、着陆坡FG和终点区GH组成，在H处安置半径为R=2.0m的圆形轨道，出口靠近但相互错开.第一过渡区和终点区的最低点在同一水平地面上，出发区距地面的高度=8.4m，跳台最高点E和着陆坡最高点F离地面的高度均为=4.0m，脊陆坡坡度37°.运动员从助滑坡顶端B由静止滑下，离开跳台在空中完成预定动作后到达F点正上方以水平速度v=4.0m/s飞出，在落到倾斜雪道FG上时，运动员靠改变姿势进行缓冲使自己只保留沿斜面的分速度而不弹起.假设运动员连同滑雪板的总质量m= 100kg，除缓冲外运动员可视为质点，滑雪板与雪道GH 的动摩擦因数μ=0.2，不计其余滑道和空气的阻力，sin37°=0.6，cos37°=0.8，求：

(1)运动员到达F点正上方时离地面的高度h；

(2)运动员在倾斜雪道FG上滑行的距离；

(3)若运动员能够不脱离圆形轨道顺利通过最高点，雪道GH的最大长度.

Answer 1

【答案】（1）7.6m（2）0.67m（3）4.04m

【解析】试题分析：运动员连同滑雪板从B 点运动到F 点正上方过程，根据机械能守恒定律即可求出运动员到达F点正上方时离地面的高度h；设运动员落在倾斜雪道K点做平抛运动，根据平抛规律即可求出运动员在倾斜雪道FG上滑行的距离；运动员落在倾斜雪道K 点时，对运动进行分解根据运动学公式和圆周运动公式再结合动能定理即可解题。

（1）运动员连同滑雪板从B 点运动到F 点正上方过程，

根据机械能守恒定律得：

代入数据解得：

(2) 设运动员落在倾斜雪道K点，离地高度为h1

根据平抛运动规律得：

位移关系为：

代入数据后解得：h1=0.4m或5.8m (不合题意)

运动员在倾斜雪道 FG上滑行的距离

(3)运动员落在倾斜雪道K 点保留沿斜面的速度：

竖直方向有：

代入数据后解得： =10.4m/s

当运动员恰好不脱离圆形轨道通过最高点时：

从K 点运动到M 点过程，根据动能定理得：

代入数据后解得：l=4.04m

运动员不脱离圆形轨道顺利通过最高点，雪道GH的最大长度为4.04m.