题目内容
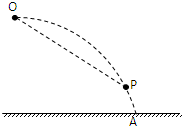如图所示，某物体自空间O点以水平初速度v0抛出，落在地面上的A点，其轨迹为一抛物线．现仿此抛物线制作一个光滑滑道并固定在与OA完全重合的位置上，然后将此物体从O点由静止释放，受微小扰动而沿此滑道滑下，在下滑过程中物体未脱离滑道．P为滑道上一点，OP连线与竖直方向成45°角，则此物体（ ）分析：若做平抛运动，OP连线与竖直方向成45°角，所以竖直分位移与水平分位移大小相等，根据时间可求出竖直方向的分速度和速度的大小和方向，若从O点由静止释放，受微小扰动而沿此滑道滑下，则物体做圆周运动，且运动过程中只有重力做功，速度方向沿切线方向．
解答：解：竖直分位移与水平分位移大小相等，有v0t=
gt2，t=
，竖直方向上的分速度vy=gt=2v0．设瞬时速度方向与水平方向成θ角，则tanθ=
=2，
从O到P做平抛运动的时间为
，则做圆周运动时，时间不为
，故A错误；
若从O点由静止释放，受微小扰动而沿此滑道滑下，运动到P点，根据动能定理得：
mv2=mgh
而平抛运动时vy2=2gh
解得：v=2v0，故D正确．
物体经过P点时，速度的水平分量为vx=vcosθ=2v0
=
v0，故B正确，C错误；
故选BD．
| 1 |
| 2 |
| 2v0 |
| g |
| vy |
| v0 |
从O到P做平抛运动的时间为
| 2v0 |
| g |
| 2v0 |
| g |
若从O点由静止释放，受微小扰动而沿此滑道滑下，运动到P点，根据动能定理得：
| 1 |
| 2 |
而平抛运动时vy2=2gh
解得：v=2v0，故D正确．
物体经过P点时，速度的水平分量为vx=vcosθ=2v0
| ||
| 5 |
2
| ||
| 5 |
故选BD．
点评：解决本题的关键掌握处理平抛运动的方法，平抛运动可分解为水平方向上的匀速直线运动和竖直方向上的自由落体运动．且分运动与合运动具有等时性．
练习册系列答案
相关题目
用数字计时器测量滑块通过光电门的时间，从而计算滑块通过光电门时的速度。测量时，在滑块上插一块挡光条，如图丙所示。挡光条前沿经过光电门时开始计时，后沿经过光电门时计时停止，计时器上显示的就是滑块发生位移l所用的时间。
随下落的高度h变化的图象，下列各图中正确的是：
用数字计时器测量滑块通过光电门的时间，从而计算滑块通过光电门时的速度。测量时，在滑块上插一块挡光条，如图丙所示。挡光条前沿经过光电门时开始计时，后沿经过光电门时计时停止，计时器上显示的就是滑块发生位移l所用的时间。
随下落的高度h变化的图象，下列各图中正确的是：
用数字计时器测量滑块通过光电门的时间，从而计算滑块通过光电门时的速度。测量时，在滑块上插一块挡光条，如图丙所示。挡光条前沿经过光电门时开始计时，后沿经过光电门时计时停止，计时器上显示的就是滑块发生位移l所用的时间。
随下落的高度h变化的图象，下列各图中正确的是：
随下落的高度h变化的图象，下列各图中正确的是：
用数字计时器测量滑块通过光电门的时间，从而计算滑块通过光电门时的速度。测量时，在滑块上插一块挡光条，如图丙所示。挡光条前沿经过光电门时开始计时，后沿经过光电门时计时停止，计时器上显示的就是滑块发生位移l所用的时间。
随下落的高度h变化的图象，下列各图中正确的是：