题目内容
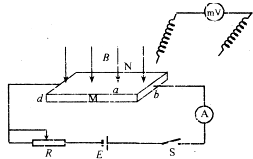 在第三次工业革命的今天,新材料的发现和运用尤为重要.我国某科研机构发现一种新型的半导体材料,目前已经知道这种半导体材料的载流子(参与导电的“带电粒子”)的电荷量的值是e(电子电量的绝对值),但不知道它的电性和载流子的数密度n(单位体积中载流子的数量).为了测定这种材料中的载流子是带正电还是带负电,以及载流子的数密度,科学家把这种材料先加工成一块偏平的六面体样品,这块样品的长、宽和厚度分别为a、b、d(如图中所示).现将这块样品接入电路中,且把靠外的偏平面标记为M,靠里的偏平面标记为N,然后在垂直于大平面的方向加上一个磁感应强度大小为B的匀强磁场.接通电键S,调节可变电阻R.使电路中产生合适的电流.然后用电压表判定M、N两个面的电势高低并测定M、N间的电压(也叫霍耳电压),从而得到这种半导体材料载流子的电性和数密度.
在第三次工业革命的今天,新材料的发现和运用尤为重要.我国某科研机构发现一种新型的半导体材料,目前已经知道这种半导体材料的载流子(参与导电的“带电粒子”)的电荷量的值是e(电子电量的绝对值),但不知道它的电性和载流子的数密度n(单位体积中载流子的数量).为了测定这种材料中的载流子是带正电还是带负电,以及载流子的数密度,科学家把这种材料先加工成一块偏平的六面体样品,这块样品的长、宽和厚度分别为a、b、d(如图中所示).现将这块样品接入电路中,且把靠外的偏平面标记为M,靠里的偏平面标记为N,然后在垂直于大平面的方向加上一个磁感应强度大小为B的匀强磁场.接通电键S,调节可变电阻R.使电路中产生合适的电流.然后用电压表判定M、N两个面的电势高低并测定M、N间的电压(也叫霍耳电压),从而得到这种半导体材料载流子的电性和数密度.(1)当M的电势比N的电势低时,材料中的载流子带
(2)为了测定载流子的数密度n,除题目中已给出的数据外,还需要测定的物理量有(写出物理量的含义并设定相应的符号)
(3)根据题设条件和你测定的物理量,写出载流子的数密度的表达式n=
分析:定向移动的电子在磁场中受洛伦兹力发生偏转,在上下表面间形成电势差,最终电子在电场力和洛伦兹力作用下处于平衡,根据平衡求出单位体积内导电的载流子的数密度.
解答:解:(1)M的电势比N的电势低,说明N极板带正电荷,结合左手定则可知,载流子带负电,导致M极板带负电;
(2)(3)载流子的洛伦兹力与电场力平衡,即:
F洛=F电
evB=e
故U=Bbv;
根据电流的微观表达式,有:I=nebdv
联立解得得n=
.
根据电阻定律,结合闭合电路欧姆定律,确定洛伦兹力与电场力的关系,还要测量MN间的电压U与通过的电流I;
故答案为:(1)负;(2)电路中的电流强度I,MN间电压U;(3)n=
.
(2)(3)载流子的洛伦兹力与电场力平衡,即:
F洛=F电
evB=e
| U |
| b |
故U=Bbv;
根据电流的微观表达式,有:I=nebdv
联立解得得n=
| BI |
| Ued |
根据电阻定律,结合闭合电路欧姆定律,确定洛伦兹力与电场力的关系,还要测量MN间的电压U与通过的电流I;
故答案为:(1)负;(2)电路中的电流强度I,MN间电压U;(3)n=
| BI |
| Ued |
点评:解决本题的关键掌握电流的微观表达式,以及知道最终电子在电场力和洛伦兹力作用下处于平衡.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 利用下列器材设计实验研究三力平衡的规律:
利用下列器材设计实验研究三力平衡的规律: