题目内容
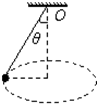如图所示，小球被细线悬挂在天花板上的O点，在水平面内做匀速圆周运动，运动中悬线与竖直方向的夹角为θ，细线长度为L．用g表示当地的重力加速度，试求小球运动的周期．分析：小球在水平面做匀速圆周运动，由重力和绳子的拉力的合力提供向心力，根据牛顿第二定律求解小球转动的周期．
解答：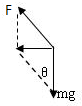
解：小球受重力mg和悬线的拉力F而在水平面内作匀速圆周运动，其合力提供向心力，如图所示．
根据数学知识得知，圆周的半径 R=Lsinθ
由牛顿第二定律得：mgtanθ=m
R
解得 T=2π
答：小球运动的周期为2π
．
解：小球受重力mg和悬线的拉力F而在水平面内作匀速圆周运动，其合力提供向心力，如图所示．根据数学知识得知，圆周的半径 R=Lsinθ
由牛顿第二定律得：mgtanθ=m
| 4π2 |
| T2 |
解得 T=2π
|
答：小球运动的周期为2π
|
点评：本题是圆锥摆问题，关键是分析小球的受力情况，确定向心力的来源．注意小球圆周运动的半径R与摆长L不同．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示，小球被轻质细绳系住斜吊着放在静止的光滑斜面上，设小球质量m=1kg，斜面倾角α=30°，悬线与竖直方向夹角θ=30°，光滑斜面的质量为3kg，置于粗糙水平面上．g=10m/s2．
把两个大小相同、质量不等的金属球用细线连接，中间夹一被压缩了的轻弹簧，置于光滑的水平桌面上，如图所示，烧断细线，观察两球的运动情况，进行必要的测量，验证物体间相互作用时动量守恒．①需测量的数据是：
