题目内容
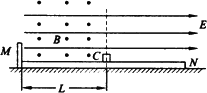
(功能关系在混合场内的应用)如图所示,MN是一固定在水平地面上足够长的绝缘平板(左侧有挡板),整个空间有平行于平板向右、场强为E=2 N/C的匀强电场,在板上C点的左侧有一个垂直于纸面向外、磁感应强度为B=1T的匀强磁场,一个质量为m=4×10-3 kg、带负电的小物块,带电量q=10-2 C,从C点由静止开始向左先做加速运动再做匀速运动.当物体碰到左端挡板后被弹回,若在碰撞瞬间将电场改为竖直向下,大小不变.小物块返回时在磁场中恰做匀速运动,已知平板MC部分的长度为L=5 m,物块与平板间的动摩擦因数为μ=0.2,求:
(1)小物块向左运动过程中克服摩擦力做的功Wf;
(2)小物块与左端挡板碰撞过程损失的机械能ΔE;
(3)小物块从与左挡板碰后到最终静止所用时间t;
(4)整个过程中由于摩擦产生的热量Q.
答案:
解析:
解析:
|
解析:设小物块向左匀速运动时的速度大小为 v1,由平衡条件有
设小物块在向左运动过程中克服摩擦力做的功为 W,由动能定理有
由①②式解得 (2)设小物块返回时在磁场中匀速运动的速度大小为v2,与右端挡板碰撞过程损失机构能为
由③⑤⑥式解得 (3)小物块由M到C匀速运动,时间为 小物块由 C到静止匀减速运动,时间为 总时间为 t=t1+t2=4.5 s ⑩(4)对全过程,由能量守恒定律有
(或 由⑤⑧式解得 评分标准:①式 2分,其余各1分,共14分 |

练习册系列答案
相关题目