题目内容
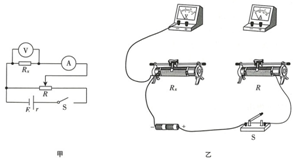
18.打点计时器是高中物理中重要的实验仪器,下图中甲、乙两种打点计时器是高中物理实验中常用的,请回答下列问题: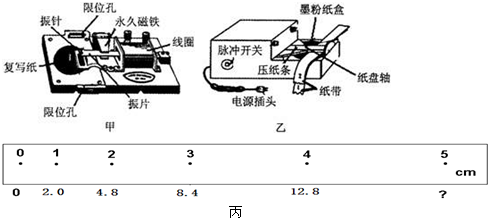
(1)图乙是电火花(填“电磁”或“电火花”)打点计时器,电源采用的是交流220v(“交流220v”、“交流4-6v”、四节干电池).
(2)在某次实验中,物体拖动纸带做匀加速直线运动,打点计时器所用的电源频率为50Hz,实验得到的一条纸带如图所示,纸带上每相邻的两个计数点之间都有4个点未画出.按时间顺序取0、1、2、3、4、5六个计数点,实验中用直尺量出各计数点到0点的距离如图丙所示(单位:cm)
①在计数点1所代表的时刻,纸带运动的瞬时速度V1=0.24m/s(保留两位有效数字)
②该同学在测量的时候没有将计数点5的数值记录下来,根据前面的数值可以算出计数点5到0点距离为18.0cm
③纸带运动的加速度a=0.80m/s2(保留两位有效数字).如果当时电网中的频率变为51HZ,而做实验的同学并不知道,那么加速度的测量值与实际值比较偏小 (填“偏大”,“偏小”或“不变”)
(3)在研究匀变速直线运动的实验中,算出小车经过各计数点的瞬时速度,为了计算加速度,合理的方法是C
A.根据任意两计数点的速度用公式a=$\frac{△v}{△t}$算出加速度
B.根据实验数据画出v-t图象,量取其倾角,由公式a=tanα求出加速度
C.根据实验数据画出v-t图象,由图象上相距较远的两点所对应的速度、时间用公式a=$\frac{△v}{△t}$算出加速度?
D.依次算出通过连续两计数点间的加速度,算出平均值作为小车的加速度?
分析 根据某段时间内的平均速度等于中间时刻的瞬时速度求出计数点1的瞬时速度,根据连续相等时间内的位移之差是一恒量求出加速度.
根据周期的测量误差,结合a=$\frac{△x}{{T}^{2}}$ 得出加速度的测量误差.
通过题目给出的数据作出速度-时间图象,解出其斜率即是小车的加速度.
解答 解:(1)图乙是电火花打点计时器,电源采用交流220V.
(2)计数点1的瞬时速度v1=$\frac{{x}_{02}}{2T}$=$\frac{0.048}{2×0.1}$m/s=0.24m/s.
由纸带数据,可知,△x=0.8cm=0.008m;
依据△x=x45-x34,那么x5=18.0cm;
根据△x=aT2得,
加速度a=$\frac{0.008}{0.{1}^{2}}$=0.80m/s2.
如果当时电网中频率变成51Hz,而做实验的同学并不知道,则周期的测量值偏大,
根据a=$\frac{△x}{{T}^{2}}$ 知,加速度的测量值偏小.
(3)AC、在处理实验数据时,如果只使用其中两个数据,由于偶然误差的存在可能会造成最后误差较大;所以我们可以根据实验数据画出v-t图象,考虑到误差,不可能是所有点都整齐的排成一条直线,连线时,应该尽量使那些不能画在线上的点均匀地分布在线的两侧,这样图线上会舍弃误差较大的点,由图线上任意两点所对应的速度及时间,用公式a=$\frac{△v}{△t}$算出加速度,所以误差小;故A错误,C正确.
B、根据实验数据画出v-t图象,当纵坐标取不同的标度时,图象的倾角就会不同,所以量出其倾角,用公式a=tanα算出的数值并不是加速度,故B错误.
D、这种方法是不对的,因为根本就不知道加速度是一个什么函数,如果是一个变化值这种方法完全是错误的,除非你能确定加速度是什么函数,故D错误.
故答案为:(1)电火花,交流220V,(2)0.24,18.0,0.80,偏小;(3)C.
点评 解决本题的关键掌握纸带的处理方法,会通过纸带求解瞬时速度和加速度,关键是匀变速直线运动推论的运用.
在实验中处理数据的方法较多,而图象法往往是一种比较准确的解题方法.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案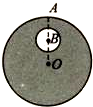 如图所示,地球半径为R,O为球心,A为地球表面上的点,B为0、A连线间的中点.设想在地球内部挖掉一以B为圆心,半径为$\frac{R}{4}$的球,忽略地球自转影响,将地球视为质量分布均匀的球体.则挖出球体后A点的重力加速度与挖去球体前的重力加速度之比为( )
如图所示,地球半径为R,O为球心,A为地球表面上的点,B为0、A连线间的中点.设想在地球内部挖掉一以B为圆心,半径为$\frac{R}{4}$的球,忽略地球自转影响,将地球视为质量分布均匀的球体.则挖出球体后A点的重力加速度与挖去球体前的重力加速度之比为( )| A. | $\frac{15}{16}$ | B. | $\frac{31}{32}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
 如图所示,两平行金属板竖直放置,质量相等的两带电液滴1、2从左极板边缘的O点分别以一定初速度竖直向上射出,两液滴分别垂直击中右极板上的A、B两点,已知C点是右极板的下端点且AB=BC,则( )
如图所示,两平行金属板竖直放置,质量相等的两带电液滴1、2从左极板边缘的O点分别以一定初速度竖直向上射出,两液滴分别垂直击中右极板上的A、B两点,已知C点是右极板的下端点且AB=BC,则( )| A. | 液滴1、2的电荷量之比为1:2 | B. | 液滴1、2的电荷量之比为1:$\sqrt{2}$ | ||
| C. | 液滴1、2的初速度之比为2:1 | D. | 液滴1、2的初速度之比为1:$\sqrt{2}$ |
| A. | 磁体对小铁块的吸引力 | B. | 月球对登月舱的吸引力 | ||
| C. | 带电体对轻小物体的吸引力 | D. | 钢绳吊起重物,重物对钢绳的拉力 |
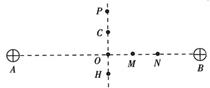 如图所示,两个点电量相等的正点电荷分别固定于绝缘水平面上的A、B两点,A、B连线的垂直平分线上有P、C、O、H四点,M、N为AB连线上的两点,已知PC=CO=OH,OM=MN,取无穷远处电势为零,下列结论中正确的是( )
如图所示,两个点电量相等的正点电荷分别固定于绝缘水平面上的A、B两点,A、B连线的垂直平分线上有P、C、O、H四点,M、N为AB连线上的两点,已知PC=CO=OH,OM=MN,取无穷远处电势为零,下列结论中正确的是( )| A. | C点和H点的电场强度相同 | |
| B. | OC与CP间的电势差相同 | |
| C. | MN两点间的电势差大于MO两点间的电势差 | |
| D. | 正检验电荷自C点由静止释放后将做加速度减小的变加速直线运动 |
 在如图所示电路中,闭合开关S,当滑动变阻器的滑动触头P向下滑动时,六个理想电表的示数都发生变化,电表A1、A2、A1、V1、V2、V3的示数分别用I1、I2、I3、U1、U2和U3表示,相应电表示数变化量的大小分别用△I1、△I2、△I3、△U1、△U2和△U3表示.下列说法正确的是( )
在如图所示电路中,闭合开关S,当滑动变阻器的滑动触头P向下滑动时,六个理想电表的示数都发生变化,电表A1、A2、A1、V1、V2、V3的示数分别用I1、I2、I3、U1、U2和U3表示,相应电表示数变化量的大小分别用△I1、△I2、△I3、△U1、△U2和△U3表示.下列说法正确的是( )| A. | I2将增大 | B. | $\frac{△{U}_{1}}{△{I}_{2}}$变大 | C. | △U3<△U2 | D. | △I2>△I1 |
| A. | 电动机的输入功率为UI | B. | 电动机的发热功率为I2R | ||
| C. | 电动机输出功率为UI-I2R | D. | 电动机功率可写作UI=I2R=$\frac{{U}^{2}}{R}$ |
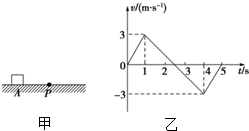 如图甲所示,质量m=4kg的物块放在光滑水平面上,在P点的左方始终受到水平向右的恒力F1的作用,在P点的右方除F1外还受到与F1在同一条直线上的水平向左的恒力F2的作用.物块从A点由静止开始运动,在0~5s内运动的v-t图象如图乙所示,由图可知下列判断正确的是( )
如图甲所示,质量m=4kg的物块放在光滑水平面上,在P点的左方始终受到水平向右的恒力F1的作用,在P点的右方除F1外还受到与F1在同一条直线上的水平向左的恒力F2的作用.物块从A点由静止开始运动,在0~5s内运动的v-t图象如图乙所示,由图可知下列判断正确的是( )| A. | t=2.5s时,物块经过P点 | |
| B. | t=5s时,物块距P点最远 | |
| C. | t=3s时,恒力F2的功率P为20 W | |
| D. | 在2~4s的过程中,F1与F2做功之和为8 J |
 为检测一个标值为5Ω的滑动变阻器,现可供使用的器材如下:
为检测一个标值为5Ω的滑动变阻器,现可供使用的器材如下: