题目内容
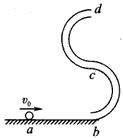
如图所示的“S”形玩具轨道,该轨道是用内壁光滑的薄壁细圆管弯成,放置在竖直平面内,轨道弯曲部 分是由两个半径相等的半圆对接而成,圆半径比细管内径大得多,轨道底端与水平地面相切,轨道在水平面上不可移动。弹射装置将一个小球(可视为质点)从a点水平弹射向b点并进入轨道,经过轨道后从最高点d水平抛出。已知小球与地面ab段间的动摩擦因数μ=0.2,不计其他机械能损失,ab段长L=1.25 m,圆的半径R=0.1 m,小球质量m=0.01 kg,轨道质量M=0.26 kg,g=10 m/s2,求:
(1)要使小球从d点抛出后不碰轨道,小球的初速度v0需满足什么条件?
(2)设小球进入轨道之前,轨道对地面的压力大小等于轨道自身的重力,当v1至少为多少时,小球经过两半圆的对接处c点时,轨道对地面的压力为零。
(3)若v0'=3 m/s,小球最终停在何处?
(1)要使小球从d点抛出后不碰轨道,小球的初速度v0需满足什么条件?
(2)设小球进入轨道之前,轨道对地面的压力大小等于轨道自身的重力,当v1至少为多少时,小球经过两半圆的对接处c点时,轨道对地面的压力为零。
(3)若v0'=3 m/s,小球最终停在何处?
解:(1)设小球到达d点处速度为vd,由动能定理,得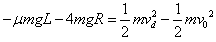 ①
①
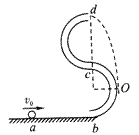
若小球由d点做平抛运动刚好经过图中的O点,则有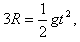 ②
②
R=vdt ③
联立①②③并代入数值得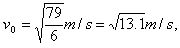 ④
④
小球的初速度v0需满足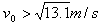 ⑤
⑤
(2)设小球到达c点处速度为vc,由动能定理,得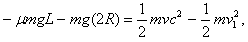 ⑥
⑥
当小球通过c点时,由牛顿第二定律得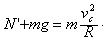 ⑦
⑦
要使轨道对地面的压力为零,则有N'=Mg ⑧
联立⑥⑦⑧并代入数值,解得小球的最小速度v1=6 m/s ⑨
(3)小球能通过d点,需满足vd≥0,由动能定理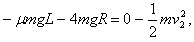 ⑩
⑩
得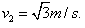
因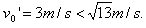 ,小球过不了d点而沿轨道原路返回
,小球过不了d点而沿轨道原路返回 
对整个过程由动能定理,有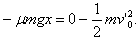

得x=2.25 m
小球最终停在a右侧0.25 m处
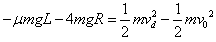 ①
① 
若小球由d点做平抛运动刚好经过图中的O点,则有
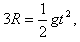 ②
②R=vdt ③
联立①②③并代入数值得
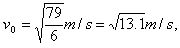 ④
④ 小球的初速度v0需满足
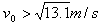 ⑤
⑤ (2)设小球到达c点处速度为vc,由动能定理,得
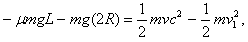 ⑥
⑥ 当小球通过c点时,由牛顿第二定律得
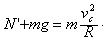 ⑦
⑦ 要使轨道对地面的压力为零,则有N'=Mg ⑧
联立⑥⑦⑧并代入数值,解得小球的最小速度v1=6 m/s ⑨
(3)小球能通过d点,需满足vd≥0,由动能定理
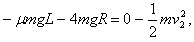 ⑩
⑩得
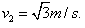
因
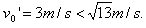 ,小球过不了d点而沿轨道原路返回
,小球过不了d点而沿轨道原路返回 对整个过程由动能定理,有
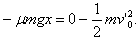
得x=2.25 m
小球最终停在a右侧0.25 m处

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 某同学玩“弹珠游戏”装置如图所示,S形管道BC由两个半径为R的
某同学玩“弹珠游戏”装置如图所示,S形管道BC由两个半径为R的