题目内容
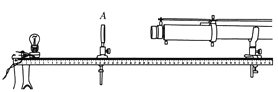
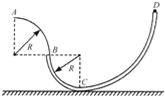
【题目】如图所示,光滑轨道固定在竖直平面内,其中BCD为细管,AB只有外轨道,AB段和BC段均为半径为R的四分之一圆弧.一质量为m的小球从管口D处静止释放,最后恰好能够到达A点,并水平抛出落到地面上.重力加速度为g求:
(1)小球到达A点速度大小vA;
(2)平抛运动的水平位移x;
(3)若小球通过C时的速度vc=![]() ,在C点轨道对球的作用力大小.
,在C点轨道对球的作用力大小.
【答案】(1)![]() .(2)2
.(2)2![]() R;(3)6mg.
R;(3)6mg.
【解析】(1)小球恰能够到达A点,由重力提供向心力,根据牛顿第二定律得:
mg=m![]()
解得小球到达A点速度为:vA=![]() .
.
(2)小球从A到落地做平抛运动,则得:
x=vAt′
![]()
解得 x=2R
(3)小球通过C时由重力和轨道的支持力的合力提供向心力,由牛顿第二定律得:
N﹣mg=m![]()
又vc=![]() ,解得 N=6mg
,解得 N=6mg

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目