题目内容
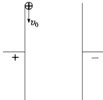（2011?广东三模）如图所示，一平行板电容器，板长为2d，板间距离为d．一带电量为q、质量为m的正离子（重力不计）以速度为v0贴近左极板，与极板平行的方向射入，恰沿右极板下边缘射出．在右极板右边空间存在垂直纸面方向的匀强磁场（未标出）．要使正离子在磁场中运动后，又能直接从右极板上边缘进入电场，则（ ）分析：粒子在电场中做类似平抛运动，离开电场后做匀速圆周运动；画出轨迹图后，根据平抛运动和匀速圆周运动的相关知识列式求解．
解答：解：A、B、粒子在电场中做类似平抛运动，离开电场后做匀速圆周运动，轨迹如图
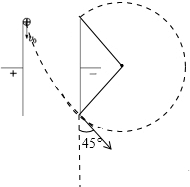
粒子带正电荷，根据左手定则，磁场方向垂直纸面向内，故A正确，B错误；
C、对于抛物线运动，速度偏向角的正切值等于位移偏向角正切值的两倍，即tanα=2tanβ=2?
=1，故α=45°，又由于tanα=
=
，故vy=v0，v=
v0；
根据几何关系，圆周运动的轨道半径为R=
d；
圆周运动中，洛伦兹力提供向心力，有qvB=m
；
解得
B=
故C正确；
D、磁场中运动时间为：t=
T=
=
=
，故D错误；
故选AC．
粒子带正电荷，根据左手定则，磁场方向垂直纸面向内，故A正确，B错误；
C、对于抛物线运动，速度偏向角的正切值等于位移偏向角正切值的两倍，即tanα=2tanβ=2?
| y |
| x |
| vy |
| vx |
| vy |
| v0 |
| 2 |
根据几何关系，圆周运动的轨道半径为R=
| 2 |
圆周运动中，洛伦兹力提供向心力，有qvB=m
| v2 |
| R |
解得
B=
| mv0 |
| qd |
故C正确；
D、磁场中运动时间为：t=
| 3 |
| 4 |
| ||||
| v |
| ||||
|
| 3πd |
| 2v0 |
故选AC．
点评：本题关键是画出运动轨迹，然后根据类平抛运动和匀速圆周运动的规律列式求解．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
（2011?广东三模）如图所示画出了匀强电场中的几条电场线，M、N是该电场中的两点，一个带正电的离子（不计重力）仅在电场力作用下由M点运动到N点，则（ ）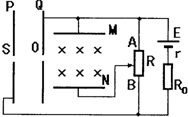
（2011?广东三模）如图所示，相距为d的水平金属板M、N的左侧有一对竖直金属板P、Q，板P上的小孔S正对板Q上的小孔O．M、N间有垂直纸面向里的匀强磁场，在小孔S处有一带负电的粒子，其重力和初速度不计．当变阻器的滑片P在AB的中点时，粒子恰能在M、N间作直线运动．则（ ）
（2011?广东三模）如图所示，MNP与RST是互相平行的倾斜导轨，导轨足够长，导轨间的距离l=0.2m，其中MN和BS与水平面的夹角为37°，ST和NP与水平面的夹角为53°，ST和NP间有磁感应强度B=1T的匀强磁场与NP和ST所在的平面垂直，导体棒ab和cd的电阻都是r=0.5Ω，导轨的电阻忽略不计，两棒与导轨间的动摩擦因素为μ=0.5，导体棒ab质量为m=0.1kg．现同时从导轨顶端释放导体棒ab和cd，经过一段时间ab和cd同时做速直线运动．（sin37°=0.6，sin53°=0.8，g=10m/s2）