题目内容
汽车正以V1=10m/s的速度在平直公路上前进,突然发现正前方S0=6米处有一辆自行车以V2=4m/s速度做同方向匀速直线运动,汽车立即刹车做加速度为a=-5m/s2的匀减速运动,则经过t=3秒,汽车与自行车相距多远?
分析:汽车刹车做匀减速运动,已知初速度和加速度,可由速度公式求出刹车到停止的时间,再根据运动学位移公式求两车的位移,得出相距的距离.
解答:解:汽车刹车到停止的时间为t0=
=
=2s
因为汽车前2S已经完全制动,速度变为0了,
则t=3s内汽车的位移等于刹车2s内的位移,为:S1=v1t0+
a
=10×2-
×5×22=10m
自行车3s内的位移:S2=v2t=4×3m=12m
所以经过t=3秒,两者之间的距离为S=S2+S0-S1=12+6-10=8m
答:经过t=3秒,汽车与自行车相距8m.
| 0-v1 |
| a |
| 0-10 |
| -5 |
因为汽车前2S已经完全制动,速度变为0了,
则t=3s内汽车的位移等于刹车2s内的位移,为:S1=v1t0+
| 1 |
| 2 |
| t | 2 1 |
| 1 |
| 2 |
自行车3s内的位移:S2=v2t=4×3m=12m
所以经过t=3秒,两者之间的距离为S=S2+S0-S1=12+6-10=8m
答:经过t=3秒,汽车与自行车相距8m.
点评:本题关键在于汽车刹车问题中,汽车匀减速直线运动的位移公式和保持静止的位移公式不同,故需要先判断运动的实际时间,再运用位移世间公式列式求解.

练习册系列答案
相关题目
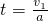 ,
,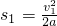 在相同时间内,自行车的前进的距离为s2=v2t,关闭油门时汽车与自行车的距离为s=s1-s2…你认为这位同学的解法是否合理?若合理,请完成计算;若不合理,请用你自己的方法算出正确结果.
在相同时间内,自行车的前进的距离为s2=v2t,关闭油门时汽车与自行车的距离为s=s1-s2…你认为这位同学的解法是否合理?若合理,请完成计算;若不合理,请用你自己的方法算出正确结果.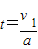 ,
,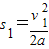 在相同时间内,自行车的前进的距离为s2=v2t,关闭油门时汽车与自行车的距离为s=s1-s2…你认为这位同学的解法是否合理?若合理,请完成计算;若不合理,请用你自己的方法算出正确结果.
在相同时间内,自行车的前进的距离为s2=v2t,关闭油门时汽车与自行车的距离为s=s1-s2…你认为这位同学的解法是否合理?若合理,请完成计算;若不合理,请用你自己的方法算出正确结果.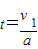 ,
,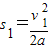 在相同时间内,自行车的前进的距离为s2=v2t,关闭油门时汽车与自行车的距离为s=s1-s2…你认为这位同学的解法是否合理?若合理,请完成计算;若不合理,请用你自己的方法算出正确结果.
在相同时间内,自行车的前进的距离为s2=v2t,关闭油门时汽车与自行车的距离为s=s1-s2…你认为这位同学的解法是否合理?若合理,请完成计算;若不合理,请用你自己的方法算出正确结果.