题目内容
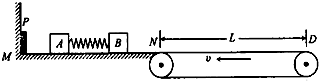 如图所示,光滑平面MN的左端M处有一弹射装置P(P为左端固定,处于压缩状态且锁定的轻质弹簧,当A与P碰撞时P立即解除锁定),有段N处与水平传送带恰平齐且很靠近传送带沿逆时针方向以恒定速率v=5m/s匀速运动墨水瓶部分长度L=4m,放在水平面上的两相同小物块A、B(均视为质点)间有一被压缩的轻质弹簧,弹性势能EP=4J,弹簧与A相连接,与B不连接,A、B与传送带间的动摩擦因数u=0.2,物块质量mA=mB=1kg.湘江A、B由静止开始释放,弹簧弹开,在B离开弹簧时,A未与P碰撞,B未滑上传送带,取g=10m/s2,求:
如图所示,光滑平面MN的左端M处有一弹射装置P(P为左端固定,处于压缩状态且锁定的轻质弹簧,当A与P碰撞时P立即解除锁定),有段N处与水平传送带恰平齐且很靠近传送带沿逆时针方向以恒定速率v=5m/s匀速运动墨水瓶部分长度L=4m,放在水平面上的两相同小物块A、B(均视为质点)间有一被压缩的轻质弹簧,弹性势能EP=4J,弹簧与A相连接,与B不连接,A、B与传送带间的动摩擦因数u=0.2,物块质量mA=mB=1kg.湘江A、B由静止开始释放,弹簧弹开,在B离开弹簧时,A未与P碰撞,B未滑上传送带,取g=10m/s2,求:(1)B滑上传送带后,向右运动的最远处与N点间的距离Sm1
(2)B从滑上传送带到返回到N端的时间t和这一过程B与传送带间摩擦产生的热能Q
(3)B回到水平面后铀浓缩被弹射装置P弹回的A上的弹簧,B与弹簧分离然后再滑上传送带,则P锁定是具有的弹性势能E满足什么条件,才能使B与弹簧分离后不再与弹簧相碰.
分析:(1)弹簧弹开的过程中,系统机械能守恒,结合动量守恒,解得A和B的速度,B滑上传送带做匀减速运动,当速度减为0时,向右运动的距离最大,由动能定理即可求解;
(2)物块B先向右做匀减速运动,直到速度减小为0,然后反方向做匀加速运动,到皮带左端时速度大小仍为vB由动量定理解出运动时间,分别求出B向右匀减速运动因摩擦力而产生的热能和向左匀加速运动因摩擦力而产生的热能,进而求出总热能.
(3)弹射装置P将能量传递给A,由能量守恒表示出A的速度vA′,由动量守恒知A,B碰撞后交换速度,B要不再返回,则
mBv‘2B>μmgL,从而求出E的条件.
(2)物块B先向右做匀减速运动,直到速度减小为0,然后反方向做匀加速运动,到皮带左端时速度大小仍为vB由动量定理解出运动时间,分别求出B向右匀减速运动因摩擦力而产生的热能和向左匀加速运动因摩擦力而产生的热能,进而求出总热能.
(3)弹射装置P将能量传递给A,由能量守恒表示出A的速度vA′,由动量守恒知A,B碰撞后交换速度,B要不再返回,则
| 1 |
| 2 |
解答:解:(1)弹簧弹开的过程中,系统机械能守恒
Ep=
mAvA2+
mBvB2
由动量守恒得:
mAvA-mBvB=0
联立以上两式解得:
vA=2m/s
vB=2m/s
B滑上传送带做匀减速运动,当速度减为0时,向右运动的距离最大.
由动能定理得:-μmBgSm=0-
mBvB2
解得:Sm=
=1m
(2)物块B先向右做匀减速运动,直到速度减小为0,然后反方向做匀加速运动,
到皮带左端时速度大小仍为vB=2m/s
由动量定理得:-μmBgt=-mBvB-mBvB
解得:t=
=2s
B向右匀减速运动因摩擦力而产生的热能为:
Q1=μmBg(
+Sm)
B向左匀加速运动因摩擦力而产生的热能为:
Q2=μmBg(
-Sm)
Q=Q1+Q2=μmBgvt=20J
(3)设弹簧p将A弹开后的速度为vA'
由能量守恒知:E=
mAv‘2A-
m
B离开弹簧后与A交换速度,则
要是B与弹簧不再相撞,则B至少滑到Q端即
mBv‘2B>μmgL
由以上三式得E>6J
答:(1)B滑上传送带后,向右运动的最远处与N点间的距离为1m;
(2)B从滑上传送带到返回到N端的时间t和这一过程B与传送带间摩擦产生的热能Q为20J.
(3)B从滑上传送带到返回到N端B回到水平面后被弹射装置P弹回的A上的弹簧,B与弹簧分离然后再滑上传送带,则P锁定是具有的弹性势能E>6J
Ep=
| 1 |
| 2 |
| 1 |
| 2 |
由动量守恒得:
mAvA-mBvB=0
联立以上两式解得:
vA=2m/s
vB=2m/s
B滑上传送带做匀减速运动,当速度减为0时,向右运动的距离最大.
由动能定理得:-μmBgSm=0-
| 1 |
| 2 |
解得:Sm=
| vB 2 |
| 2μg |
(2)物块B先向右做匀减速运动,直到速度减小为0,然后反方向做匀加速运动,
到皮带左端时速度大小仍为vB=2m/s
由动量定理得:-μmBgt=-mBvB-mBvB
解得:t=
| 2vB |
| μg |
B向右匀减速运动因摩擦力而产生的热能为:
Q1=μmBg(
| vt |
| 2 |
B向左匀加速运动因摩擦力而产生的热能为:
Q2=μmBg(
| vt |
| 2 |
Q=Q1+Q2=μmBgvt=20J
(3)设弹簧p将A弹开后的速度为vA'
由能量守恒知:E=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 A |
B离开弹簧后与A交换速度,则
| v | ′ B |
| =v | ′ A |
要是B与弹簧不再相撞,则B至少滑到Q端即
| 1 |
| 2 |
由以上三式得E>6J
答:(1)B滑上传送带后,向右运动的最远处与N点间的距离为1m;
(2)B从滑上传送带到返回到N端的时间t和这一过程B与传送带间摩擦产生的热能Q为20J.
(3)B从滑上传送带到返回到N端B回到水平面后被弹射装置P弹回的A上的弹簧,B与弹簧分离然后再滑上传送带,则P锁定是具有的弹性势能E>6J
点评:本题主要考查了机械能守恒定律、动量守恒定律及动能定理的直接应用,难度适中.

练习册系列答案
相关题目
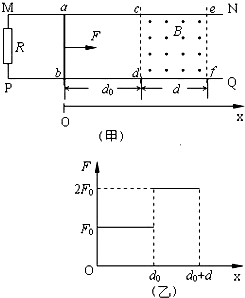 如图所示,光滑的平行水平金属导轨MN、PQ相距L,在M点和P点间连接一个阻值为R的电阻,在两导轨间cdfe矩形区域内有垂直导轨平面竖直向上、宽为d的匀强磁场,磁感应强度为B、一质量为m、电阻为r、长度也刚好为L的导体棒ab垂直置于导轨上,与磁场左边界相距d 0.现用一个水平向右的力F拉棒ab,使它由静止开始运动,棒ab离开磁场前已做匀速直线运动,棒ab与导轨始终保持良好接触,导轨电阻不计,F随ab与初始位置的距离x变化的情况如图(乙)所示,F0已知.求:
如图所示,光滑的平行水平金属导轨MN、PQ相距L,在M点和P点间连接一个阻值为R的电阻,在两导轨间cdfe矩形区域内有垂直导轨平面竖直向上、宽为d的匀强磁场,磁感应强度为B、一质量为m、电阻为r、长度也刚好为L的导体棒ab垂直置于导轨上,与磁场左边界相距d 0.现用一个水平向右的力F拉棒ab,使它由静止开始运动,棒ab离开磁场前已做匀速直线运动,棒ab与导轨始终保持良好接触,导轨电阻不计,F随ab与初始位置的距离x变化的情况如图(乙)所示,F0已知.求:

