题目内容
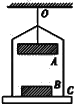
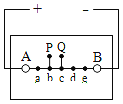
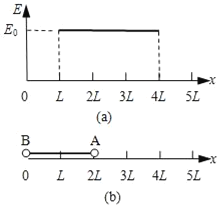
【题目】光滑绝缘水平面上有一水平向右的匀强电场,其场强大小分布如图(a)所示.两个质量均为m的带电小球A和B由长为2L的轻杆相连,组成一带电系统,球A带电量为+2q,球B带电量为﹣q.t=0时刻,带电系统由如图(b)所示位置从静止开始运动.若视小球为质点,不计轻杆的质量,求:
(1)当球B刚进入电场时,带电系统速度v1的大小;
(2)当球A刚离开电场时,带电系统速度v2的大小;
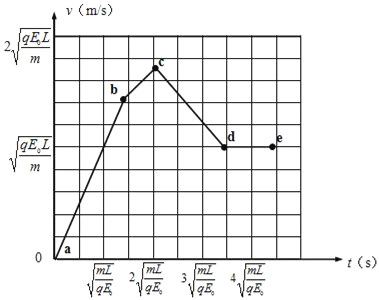
(3)通过分析、计算、推理,描述带电系统中的球B从x=0到x=5L的运动状态,并作出对应的v﹣t图.
【答案】(1)![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】
(1)设带电系统开始运动时,加速度为a1,由牛顿第二定律得:
![]()
解得:
![]()
设球B刚进入电场时,带电系统的速度为v1,由v12=2a1L得:
![]()
(2)设球B进入电场后,带电系统的加速度为a2,由牛顿第二定律得:
![]()
代入数据解得:
![]()
带电系统继续做匀加速运动.
设球A刚离开电场时的速度为v2,由v22-v12=2a2L得:
![]()
(3)设球B从静止到刚进入电场的时间为t1,(球B从x=0到x=L)则:
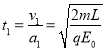
设从球B进入电场到球A离开电场经历的时间为t2,(球B从x=L 到x=2L)则:
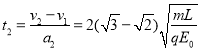
球A离开电场后,带电系统做减速运动,设加速度为a3,由牛顿第二定律得:
![]()
得
![]()
设球B运动到电场边缘(x=4L)处,速度为v3,由v32-v22=2a3×2L得:
![]()
设从球A离开电场到球B离开电场所需时间为t3,(球B从x=2 L 到x=4L)则:
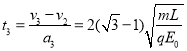
球B离开电场后(球B从x=4 L 到x=5L),就以v3一直做匀速直线运动.
描述:( 图象加文字)
a﹣b过程(球B从x=0到x=L)是静止出发,带电系统以加速度a1做匀加速运动,当球B进入电场时,速度为v1,此过程经历时间为t1,通过距离为L;
b﹣c过程(球B从x=L 到x=2L)是带电系统以加速度a2继续做匀加速运动,经历时间为t2,直到球A到达电场边缘,速度为v2,通过距离为L;
c﹣d 过程(球B从x=2 L 到x=4L)是带电系统以加速度a3做匀减速运动,经历时间t3,球B到达电场边缘,速度为v3,通过距离为2L;
d﹣e过程(球B从x=4 L 到x=5L)是带电系统离开电场,以v3做匀速直线运动,直至运动到x=5L 处,即e点.
由此可得v﹣t图象如下