题目内容
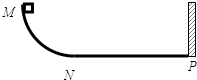 如图,MNP 为竖直面内一固定轨道,其圆弧段MN与水平段NP相切于N、P端固定一竖直挡板.M相对于N的高度为h,NP长度为s.一木块自M端从静止开始沿轨道下滑,与挡板最多发生一次碰撞,且碰撞前后速度不变,停止在水平轨道上某处.若在MN段的摩擦可忽略不计,物块与NP段轨道间的滑动摩擦因数为μ,求物块停止的地方与N点距离的可能值( )
如图,MNP 为竖直面内一固定轨道,其圆弧段MN与水平段NP相切于N、P端固定一竖直挡板.M相对于N的高度为h,NP长度为s.一木块自M端从静止开始沿轨道下滑,与挡板最多发生一次碰撞,且碰撞前后速度不变,停止在水平轨道上某处.若在MN段的摩擦可忽略不计,物块与NP段轨道间的滑动摩擦因数为μ,求物块停止的地方与N点距离的可能值( )分析:滑动摩擦力做功与物块通过的总路程有关.根据动能定理求出物块在NP上运动的总路程,再研究物块停止的地方与N点距离的可能值.
解答:解:设物块在NP上运动的总路程为S,根据动能定理得
mgh-μmgS=0
得到S=
A、若物块恰好不与挡板碰撞而停在P点时,物块停止的地方与N点距离为
.故A正确.
B、若物块与挡板碰撞一次,向左运动时停下,由物块停止的地方与N点距离为2s-
.故B正确.
C、若物块与挡板碰撞一次后,滑上MN又滑下,向右运动停下时,由物块停止的地方与N点距离为
-2s.故C正确.
D、由于物块在NP上滑行的总路程为
,物块停止的地方与N点距离与
有关,与μh无关.故D错误.
故选ABC
mgh-μmgS=0
得到S=
| h |
| μ |
A、若物块恰好不与挡板碰撞而停在P点时,物块停止的地方与N点距离为
| h |
| μ |
B、若物块与挡板碰撞一次,向左运动时停下,由物块停止的地方与N点距离为2s-
| h |
| μ |
C、若物块与挡板碰撞一次后,滑上MN又滑下,向右运动停下时,由物块停止的地方与N点距离为
| h |
| μ |
D、由于物块在NP上滑行的总路程为
| h |
| μ |
| h |
| μ |
故选ABC
点评:本题要抓住滑动摩擦力做功与路程有关这个规律.当条件不确定时,要分情况讨论,不能漏解.

练习册系列答案
相关题目
 如图,MNP为竖直面内一固定轨道,其圆弧段MN与水平段NP相切于N、P端固定一竖直挡板.M相对于N的高度为h,NP长度为s.一木块自M端从静止开始沿轨道下滑,与挡板发生一次完全弹性碰撞后停止在水平轨道上某处.若在MN段的摩擦可忽略不计,物块与NP段轨道间的滑动摩擦因数为μ,求物块停止的地方与N点距离的可能值.
如图,MNP为竖直面内一固定轨道,其圆弧段MN与水平段NP相切于N、P端固定一竖直挡板.M相对于N的高度为h,NP长度为s.一木块自M端从静止开始沿轨道下滑,与挡板发生一次完全弹性碰撞后停止在水平轨道上某处.若在MN段的摩擦可忽略不计,物块与NP段轨道间的滑动摩擦因数为μ,求物块停止的地方与N点距离的可能值.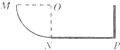 如图,MNP为竖直面内一固定轨道,其
如图,MNP为竖直面内一固定轨道,其