题目内容
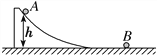
【题目】如图所示,一质量M=2 kg的带有弧形轨道的平台置于足够长的水平轨道上,弧形轨道与水平轨道平滑连接,水平轨道上静置一小球B。从弧形轨道上距离水平轨道高h=0.3 m处由静止释放一质量mA=1 kg的小球A,小球A沿轨道下滑后与小球B发生弹性正碰,碰后小球A被弹回,且恰好追不上平台。已知所有接触面均光滑,重力加速度为g。
求小球B的质量。(g取10 m/s2)
【答案】3 kg
【解析】试题分析:设小球A下滑到水平轨道上时的速度大小为v1,平台水平速度大小为v,设向右为正方向;由动量守恒定律有:
mAv1=Mv
由能量守恒定律有:
mAgh=mAv12+mBv22
联立并代入数据解得:
v1=2m/s,
v=1m/s
小球A、B碰后运动方向相反,设小球A、B的速度大小分别为v1′和v2,由题意知:
v1′=1m/s
由动量守恒定律得:
mAv1=﹣mAv1′+mBv2
由能量守恒定律有:
mAv12=mAv12+mBv22
联立并代入数据解得:mB=3kg

练习册系列答案
相关题目