题目内容
 如图所示,一个物块在与水平方向成α角的拉力F作用下,沿水平面向右做匀速直线运动.已知重力加速度g、角α和拉力F的大小,若要求出物块与水平面间的动摩擦因数,还须知道( )
如图所示,一个物块在与水平方向成α角的拉力F作用下,沿水平面向右做匀速直线运动.已知重力加速度g、角α和拉力F的大小,若要求出物块与水平面间的动摩擦因数,还须知道( )分析:先对物体近行受力分析,然后正交分解,再列方程求解,看求出的动摩擦因数表达式中哪个量还需要知道
解答:解:设物体滑动摩擦因数为μ,受的滑动摩擦力为f,受支持力为FN,受重力为mg,受力分析如图:

x轴方向:Fcosα=f
y轴方向:FN+Fsinα=mg
又:f=μFN
联立三个方程得:μ=
由上式可以看出还需知道物块的质量,故:选D

x轴方向:Fcosα=f
y轴方向:FN+Fsinα=mg
又:f=μFN
联立三个方程得:μ=
| Fcosα |
| mg-Fsinα |
由上式可以看出还需知道物块的质量,故:选D
点评:本题考查滑动摩擦力的计算,重点是正交分解然后求出支持力FN的大小,正交分解作图和列方程时一定要注重规范

练习册系列答案
相关题目
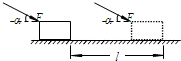 如图所示,一个物块在与水平方向成α角的恒定推力F的作用下,沿水平面向右运动一段距离l.在此过程中,恒力F对物块所做的功为( )
如图所示,一个物块在与水平方向成α角的恒定推力F的作用下,沿水平面向右运动一段距离l.在此过程中,恒力F对物块所做的功为( )| A、Fl | B、Fl sinα | C、Fl cosα | D、Fl tanα |
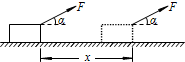 如图所示,一个物块在与水平方向成α角的拉力F作用下,沿水平面向右运动一段距离x,所用时间为t.在此过程中,拉力F对物块做功的平均功率为( )
如图所示,一个物块在与水平方向成α角的拉力F作用下,沿水平面向右运动一段距离x,所用时间为t.在此过程中,拉力F对物块做功的平均功率为( )
 C.Fxcosα
D.
C.Fxcosα
D.
