题目内容
（2011?浙江）如图甲所示，在水平面上固定有长为L=2m、宽为d=1m的金属“U”型导轨，在“U”型导轨右侧l=0.5m范围内存在垂直纸面向里的匀强磁场，且磁感应强度随时间变化规律如图乙所示．在t=0时刻，质量为m=0.1kg的导体棒以v0=1m/s的初速度从导轨的左端开始向右运动，导体棒与导轨之间的动摩擦因数为μ=0.1，导轨与导体棒单位长度的电阻均为λ=0.1Ω/m，不计导体棒与导轨之间的接触电阻及地球磁场的影响（取g=10m/s2）．
（1）通过计算分析4s内导体棒的运动情况；
（2）计算4s内回路中电流的大小，并判断电流方向；
（3）计算4s内回路产生的焦耳热．
（1）通过计算分析4s内导体棒的运动情况；
（2）计算4s内回路中电流的大小，并判断电流方向；
（3）计算4s内回路产生的焦耳热．
分析：导体棒在没有磁场区域，由于摩擦阻力做匀减速运动，由牛顿第二定律求出加速度，然后确定4s棒的运动情况．回路中前2S内没有磁通量变化，后2S内磁通量均匀变小，产生的电动势不变，则电流恒定，故由焦耳定律可求出产生的热量．
解答：解：（1）导体棒先在无磁场区域做匀减速运动，有-μmg=ma
vt=v0+at
x=v0t+
at2
代入数据解得：t=1s，x=0.5m，导体棒没有进入磁场区域．
导体棒在1s末已经停止运动，以后一直保持静止，离左端位置仍为x=0.5m
（2）前2s磁通量不变，回路电动势和电流分别为E=0，I=0
后2s回路产生的电动势为E=
=ld
=0.1V
回路的总长度为5m，因此回路的总电阻为R=5λ=0.5Ω
电流为I=
=0.2A
根据楞次定律，在回路中的电流方向是顺时针方向
（3）前2s电流为零，后2s有恒定电流，焦耳热为Q=I2Rt=0.04J
vt=v0+at
x=v0t+
| 1 |
| 2 |
代入数据解得：t=1s，x=0.5m，导体棒没有进入磁场区域．
导体棒在1s末已经停止运动，以后一直保持静止，离左端位置仍为x=0.5m
（2）前2s磁通量不变，回路电动势和电流分别为E=0，I=0
后2s回路产生的电动势为E=
| △? |
| △t |
| △B |
| △t |
回路的总长度为5m，因此回路的总电阻为R=5λ=0.5Ω
电流为I=
| E |
| R |
根据楞次定律，在回路中的电流方向是顺时针方向
（3）前2s电流为零，后2s有恒定电流，焦耳热为Q=I2Rt=0.04J
点评：法拉第电磁感应定律求感应电动势，由闭合电路殴姆定律可列出电动势与电流的关系．楞次定律是判定感应电流方向，焦耳定律可求出电阻的发热量．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
（2011?浙江）如图所示，甲、乙两人在冰面上“拔河”．两人中间位置处有一分界线，约定先使对方过分界线者为赢．若绳子质量不计，冰面可看成光滑，则下列说法正确的是（ ）
（2011?浙江）如图所示，在铁芯上、下分别绕有匝数n1=800和n2=200的两个线圈，上线圈两端与u=51sin314tV的交流电源相连，将下线圈两端接交流电压表，则交流电压表的读数可能是（ ）
（2011?浙江一模）如图所示，一平行板电容器水平放置，板间距离为d，上极板开有一小孔，质量均为m，带电荷量均为+q的两个带电小球（视为质点），其间用长为L的绝缘轻杆相连，处于竖直状态，已知d=2L，今使下端小球恰好位于小孔中，由静止释放，让两球竖直下落．当下端的小球到达下极板时，速度刚好为零．试求：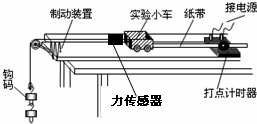
（2011?浙江模拟）1某课外兴趣小组利用下图的实验装置研究“合外力做功和物体动能变化之间的关系”以及“加速度与合外力的关系”
