题目内容
 为了测量两个质量不等的沙袋的质量,某实验小组在实验室找到了下列器材:轻质定滑轮(质量和摩擦可忽略)、砝码一套、细线、米尺、秒表,由于没有找到直接测量工具,他们决定根据已学过的物理学知识,改变实验条件进行测量,通过选择合适的变量得到线性关系,再根据图线的斜率和截距求出沙袋的质量,于是他们进行了下列操作:
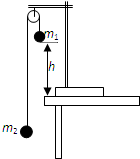
为了测量两个质量不等的沙袋的质量,某实验小组在实验室找到了下列器材:轻质定滑轮(质量和摩擦可忽略)、砝码一套、细线、米尺、秒表,由于没有找到直接测量工具,他们决定根据已学过的物理学知识,改变实验条件进行测量,通过选择合适的变量得到线性关系,再根据图线的斜率和截距求出沙袋的质量,于是他们进行了下列操作:①实验装置如图,设两边沙袋的质量分别为m1、m2;
②砝码的总质量为△m=0.5kg,实验小组先从△m中取出质量为m′的砝码放在m1沙袋中,剩余砝码都放在m2沙袋中,发现m1下降m2上升;
③用米尺测出沙袋运动的距离h,用秒表测出沙袋的运动时间t,则可知沙袋的加速度大小为a=
| 2h |
| t2 |
| 2h |
| t2 |
④改变m′,测量加速度a,得多组(m′,a)数据,作出“a-m′”图线;
⑤该小组成员得到图线的斜率为k=4m/kg?s2,截距为b=2,请你算出沙袋的质量m1=
3
3
kg,m2=1.5
1.5
kg.(其中g取10m/s2)分析:(1)质量为m1的沙袋从静止开始下降做匀加速直线运动,根据下降的距离h和时间,由位移公式求出其加速度.
(2)根据牛顿第二定律对m2、m1分别研究,得出△m与a的关系式,根据数学知识分析图线的斜率与截距的意义,求解两个沙袋的质量.
(2)根据牛顿第二定律对m2、m1分别研究,得出△m与a的关系式,根据数学知识分析图线的斜率与截距的意义,求解两个沙袋的质量.
解答:解:(3)由题,质量为m1的沙袋从静止开始下降做匀加速直线运动,由h=
at2得,
a=
.
(5)根据牛顿第二定律得:
对m1及砝码:(m1+m′)g-T=(m1+m′)a
对m2及砝码:T-(m2+△m-m′)g=(m2+△m-m′)a
联立解得:a=
g+
.
根据数学知识得知:“a~△m”图线斜率k=
,截距b=
.
将△m=0.5kg,g=10m/s2,k=4m/kg?s2,b=2m/s2,代入解得:m1=3kg,m2=1.5kg.
故答案为:
,3kg,1.5 kg
| 1 |
| 2 |
a=
| 2h |
| t2 |
(5)根据牛顿第二定律得:
对m1及砝码:(m1+m′)g-T=(m1+m′)a
对m2及砝码:T-(m2+△m-m′)g=(m2+△m-m′)a
联立解得:a=
| (m1-m2-△m) |
| m1+m2+△m |
| 2gm′ |
| m1+m2+m |
根据数学知识得知:“a~△m”图线斜率k=
| 2g |
| m1+m2+△m |
| (m1-m2-△m)g |
| m1+m2+△m |
将△m=0.5kg,g=10m/s2,k=4m/kg?s2,b=2m/s2,代入解得:m1=3kg,m2=1.5kg.
故答案为:
| 2h |
| t2 |
点评:本题是加速度不同的连接体问题,运用隔离法研究加速度,得到a与△m的关系式,再根据图线的数学意义求解两个沙袋的质量.

练习册系列答案
相关题目
 (2011?台州模拟)为了测量两个质量不等沙袋的质量,由于没有可直接测量的工具(如天平、弹簧秤等),某实验小组应用下列器材测量:轻质定滑轮(质量和摩擦可忽略)、一套总质量为m=0.5kg砝码,细线、米尺、秒表,他们根据所学的物理知识改变实验条件进行多次测量,选择合适的变量得到线性关系,作出图线并根据图线的斜率和截距求出沙袋的质量(g取10m/s2).具体操作如下:
(2011?台州模拟)为了测量两个质量不等沙袋的质量,由于没有可直接测量的工具(如天平、弹簧秤等),某实验小组应用下列器材测量:轻质定滑轮(质量和摩擦可忽略)、一套总质量为m=0.5kg砝码,细线、米尺、秒表,他们根据所学的物理知识改变实验条件进行多次测量,选择合适的变量得到线性关系,作出图线并根据图线的斜率和截距求出沙袋的质量(g取10m/s2).具体操作如下:
 ”)图线;
”)图线; 为了测量两个质量不等沙袋的质量,由于没有可直接测量的工具(如天平、弹簧秤等),某实验小组应用下列器材测量:轻质定滑轮(质量和摩擦可忽略)、一套总质量为m=0.5kg砝码,细线、米尺、秒表,他们根据所学的物理知识改变实验条件进行多次测量,选择合适的变量得到线性关系,作出图线并根据图线的斜率和截距求出沙袋的质量(g取10m/s2).具体操作如下:
为了测量两个质量不等沙袋的质量,由于没有可直接测量的工具(如天平、弹簧秤等),某实验小组应用下列器材测量:轻质定滑轮(质量和摩擦可忽略)、一套总质量为m=0.5kg砝码,细线、米尺、秒表,他们根据所学的物理知识改变实验条件进行多次测量,选择合适的变量得到线性关系,作出图线并根据图线的斜率和截距求出沙袋的质量(g取10m/s2).具体操作如下: