题目内容
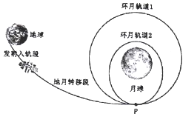
【题目】2018年12月12日,我国发射的“嫦娥四号”探测器进入环月轨道1,12月30日实施变轨进入环月轨道2.其飞行轨道如图所示,p点为两轨道的交点。如果嫦娥四号探测器在环月轨道1和环月轨道2上运动时,只受到月球的万有引力作用,环月轨道1为圆形轨道,环月轨道2为椭圆轨道。则以下说法正确的是( )
A. 若已知嫦娥四号探测器环月轨道1的半径、运动周期和引力常量,则可以计算出月球的密度
B. 若已知婦娥四号探测器环月轨道2的近月点到月球球心的距离、运动周期和引力常量,则可以计算出月球的密度
C. 嫦娥四号探测器在环月轨道2上经过p点的速度小于在环月轨道1上经过P点的速度
D. 娀四号探测器在环月轨道2时,从近月点运动向远月点P的过程中,加速度变大
【答案】C
【解析】
由万有引力提供向心力可得:![]() ,则圆轨道的周期公式
,则圆轨道的周期公式![]() ,则可计算出月球质量M,但月球半径R未知,所以算不出月球密度,故A错误;因为2轨道为椭圆轨道用不了圆轨道的周期公式,且月球半径R未知,同理计算不出月球密度,故B错误;探测器在1轨道的P减速后才能变轨到2轨道,故C正确;由近月点向远月点P运动过程中,探测器与月心距离增大,则引力减小,由牛顿第二定律加速度应变小,故D错误。
,则可计算出月球质量M,但月球半径R未知,所以算不出月球密度,故A错误;因为2轨道为椭圆轨道用不了圆轨道的周期公式,且月球半径R未知,同理计算不出月球密度,故B错误;探测器在1轨道的P减速后才能变轨到2轨道,故C正确;由近月点向远月点P运动过程中,探测器与月心距离增大,则引力减小,由牛顿第二定律加速度应变小,故D错误。

练习册系列答案
相关题目





