题目内容
20.一物体做匀速圆周运动,写出(1)周期T与频率f的关系式
(2)角速度w与周期T的关系式
(3)线速度v与角速度w的关系式.
分析 直接根据线速度、角速度、周期的定义以及角度的定义出发,分析各个量之间的关系.
解答 解:(1)周期T与频率f的关系式为:f=$\frac{1}{T}$;
(2)角速度:ω=$\frac{△θ}{△t}$,故$ω=\frac{2π}{T}$;
(3)角速度:ω=$\frac{△θ}{△t}$,
线速度:v=$\frac{2πr}{T}$,
故线速度与角速度的关系为:v=rω,
答:1)周期T与频率f的关系式为f=$\frac{1}{T}$;
(2)角速度ω与周期T的关系式为$ω=\frac{2π}{T}$;
(3)线速度v与角速度ω的关系式为v=rω.
点评 正确理解并掌握线速度的定义和角速度的定义式,正确推导各量之间的关系是解决本题的关键.

练习册系列答案
相关题目
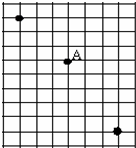
11. 如图所示,半径为R,内壁光滑的空心圆筒放在地面上,将两个重为G,半径都为r(R<2r<2R)的球放在圆筒中,下列说法不正确的是( )
如图所示,半径为R,内壁光滑的空心圆筒放在地面上,将两个重为G,半径都为r(R<2r<2R)的球放在圆筒中,下列说法不正确的是( )
 如图所示,半径为R,内壁光滑的空心圆筒放在地面上,将两个重为G,半径都为r(R<2r<2R)的球放在圆筒中,下列说法不正确的是( )
如图所示,半径为R,内壁光滑的空心圆筒放在地面上,将两个重为G,半径都为r(R<2r<2R)的球放在圆筒中,下列说法不正确的是( )| A. | 地面对A的弹力等于2G | B. | 筒壁对A的弹力等于对球B的弹力 | ||
| C. | 两球间的弹力一定大于G | D. | 球B对筒壁的压力F一定小于G |
8.(1)使用打点计时器来分析物体运动情况的实验中:有如下基本步骤:
A、把打点计时器固定在桌子上 B、安好纸带
C、松开纸带让物体带着纸带运动 D、接通低压交流电源
E、取下纸带 F、断开开关
这些步骤正确的排列顺序为ABDCFE.
(2)用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点.其相邻点间的距离如图所示,每两个相邻的计数点之间还有4个打印点未画出.
①试根据纸带上各个计数点间的距离,计算出打下B、C、D、E、F五个点时小车的瞬时速度,并将各个速度值填入下表要求保留3位有效数字.
②小车加速度为0.80m/s2.
A、把打点计时器固定在桌子上 B、安好纸带
C、松开纸带让物体带着纸带运动 D、接通低压交流电源
E、取下纸带 F、断开开关
这些步骤正确的排列顺序为ABDCFE.
(2)用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点.其相邻点间的距离如图所示,每两个相邻的计数点之间还有4个打印点未画出.

①试根据纸带上各个计数点间的距离,计算出打下B、C、D、E、F五个点时小车的瞬时速度,并将各个速度值填入下表要求保留3位有效数字.
| VB | VC | VD | VE | FF | |
| 数值(m/s) | 0.479 | 0.560 | 0.640 |
5.关于加速度与速度的关系,正确的说法是( )
| A. | 加速度为零的物体,其速度一定为零 | |
| B. | 加速度减小时,速度一定减小 | |
| C. | 2 m/s2的加速度比-4m/s2的加速度小 | |
| D. | 速度为零,加速度为零 |
 如图所示,A,B两物体叠放在一起,由静止释放后沿光滑斜面下滑,且始终保持相对静止,B上表面水平,则物体B的受力示意图是( )
如图所示,A,B两物体叠放在一起,由静止释放后沿光滑斜面下滑,且始终保持相对静止,B上表面水平,则物体B的受力示意图是( )


 (1)在做“研究平抛物体的运动”实验时,除了木板、小球、斜槽、铅笔、图钉之外,下列器材中还需要的是BE
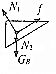
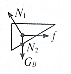
(1)在做“研究平抛物体的运动”实验时,除了木板、小球、斜槽、铅笔、图钉之外,下列器材中还需要的是BE 在“探究求合力的方法”时,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的两根细绳,实验时,需要两次拉伸橡皮条,一次是通过两细绳用两个弹簧秤互成角度地拉橡皮条,另一次是用一个弹簧秤通过细绳拉橡皮条.试回答下列问题:
在“探究求合力的方法”时,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的两根细绳,实验时,需要两次拉伸橡皮条,一次是通过两细绳用两个弹簧秤互成角度地拉橡皮条,另一次是用一个弹簧秤通过细绳拉橡皮条.试回答下列问题: