题目内容
16.如图所示,在直角坐标系的第Ⅱ象限和第Ⅳ象限中的直角三角形区域内,分布着磁感应强度均为B=5.0×10-2T的匀强磁场,方向分别垂直纸面向外和向里.质量为m=6.64×10-27㎏、电荷量为q=+3.2×10-19C的α粒子(不计α粒子重力),由静止开始经加速电压为U=1205V的电场(图中未画出)加速后,从坐标点M(-4,$\sqrt{2}$)处平行于x轴向右运动,并先后通过匀强磁场区域.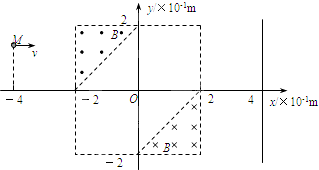
(1)请你求出α粒子在第Ⅱ象限内做圆周运动的半径和圆心坐标;
(2)请你求出α粒子在第Ⅱ象限磁场区域偏转所用的时间;
(3)请你在图中画出α粒子从直线x=-4到直线x=4之间的运动轨迹,并在图中标明轨迹与直线x=4交点的坐标.
分析 (1)带电粒子由静止开始经加速电压为U=1250V的电场时,获得了速度,根据动能定理可求出带电粒子的速度.进入磁场后由洛伦兹力提供向心力,由牛顿第二定律求得粒子在磁场中的运动半径.
(2)由几何知识求出粒子经过磁场时轨迹所对应的圆心角α,由t=$\frac{α}{2π}$T求解运动时间.
(3)由几何关系画出粒子从直线x=-4到直线x=4之间的运动轨迹.
解答 解:(1)α粒子在电场中被加速,由动能定理得:
$qU=\frac{1}{2}m{v^2}$,
α粒子在磁场中偏转,洛伦兹力提供向心力,由牛顿第二定律得:
$qvB=m\frac{v^2}{r}$,
解得:$r=\frac{1}{B}\sqrt{\frac{2mU}{q}}=\frac{1}{0.05}\sqrt{\frac{{2×6.64×{{10}^{-27}}×1205}}{{3.2×{{10}^{-19}}}}}=\sqrt{2}×{10^{-1}}$m≈0.1414m,
又因为粒子进入磁场时离x轴的距离恰好等于r,所以粒子做圆周运动的圆心坐标为(-0.2,0);
(2)带电粒子在磁场中的运动周期为:$T=\frac{2πr}{v}=\frac{2πm}{qB}$,
α粒子在磁场中偏转的弧度为$\frac{π}{4}$,在磁场中的运动时间为:
$t=\frac{1}{8}T=\frac{πm}{4qB}=\frac{{3.14×6.64×{{10}^{-27}}}}{{4×3.2×{{10}^{-19}}×5×{{10}^{-2}}}}=3.25×{10^{-7}}$s;
(3)粒子运动轨迹如图所示: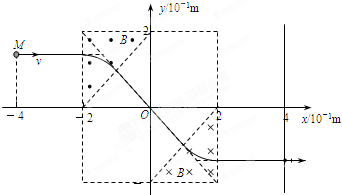
答:(1)α粒子在第Ⅱ象限内做圆周运动的半径为0.1414m,圆心坐标为(-0.2,0);
(2)α粒子在第Ⅱ象限磁场区域偏转所用的时间为3.25×10-7s;
(3)轨迹如图所示.
点评 本题中带电粒子在复合场中运动的问题,在电场中运用动能定理求解速度,在磁场中关键是画出轨迹,由几何知识求出轨迹的圆心角,确定时间,都是常规思路.

 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案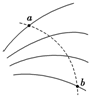 如所示,图中实线是一簇未标明方向的电场线,虚线是某带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点,若带电粒子在运动过程中只受电场力作用,根据此图能做出正确的判断的是( )
如所示,图中实线是一簇未标明方向的电场线,虚线是某带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点,若带电粒子在运动过程中只受电场力作用,根据此图能做出正确的判断的是( )| A. | 带电粒子所带电荷的正负 | |
| B. | 带电粒子在a、b两点受力方向 | |
| C. | 带电粒子在a、b两点加速度何处较大 | |
| D. | 带电粒子在a、b两点的场强的方向 |
| A. | 第2秒内的平均速度为15m/s | |
| B. | 第7秒内的位移为65m | |
| C. | 后一秒的位移总比前一秒的位移多5m | |
| D. | 前一秒的平均速度总比后一秒的平均速度小10m/s |
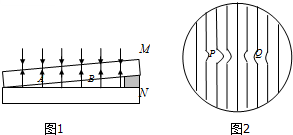 如图1所示用单色光检查工件上表面是否平整,观察到的现象如图所示的条纹中的P和Q分别为待测工件在A和B处的情况,这说明( )
如图1所示用单色光检查工件上表面是否平整,观察到的现象如图所示的条纹中的P和Q分别为待测工件在A和B处的情况,这说明( )| A. | M为待测工件 | |
| B. | N的上表面B处向上凹陷 | |
| C. | M的上表面A处向下凹陷 | |
| D. | 若减小二工件间空气膜夹角,则条纹间距变密 |
| A. | 元电荷就是电子 | |
| B. | 点电荷是真实存在的 | |
| C. | 体积很小的带电体就是点电荷,较大的带电体,不能看成点电荷 | |
| D. | 一个带电体能否看成点电荷,不是看它的尺寸的绝对值,而是看它在研究的问题中形状和大小对相互作用力的影响是否能忽略不计 |
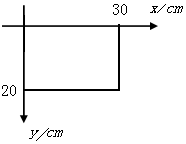 在“研究平抛运动”实验中,如图所示,O为抛出点,A(30cm,20cm)为物体运动过程中通过的一点,则物体平抛的初速度为1.5m/s.(g取10m/s2)
在“研究平抛运动”实验中,如图所示,O为抛出点,A(30cm,20cm)为物体运动过程中通过的一点,则物体平抛的初速度为1.5m/s.(g取10m/s2)