Question

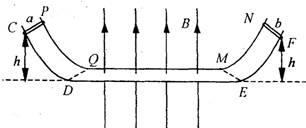
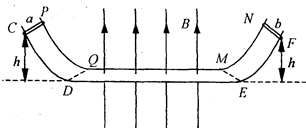
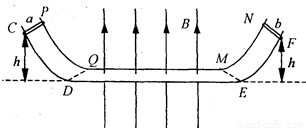
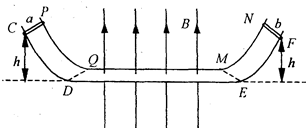如图所示，PQMN与CDEF为两根足够长的固定平行金属导轨，导轨间距为L．PQ、MN、CD、EF为相同的弧形导轨；QM、DE为足够长的水平导轨．导轨的水平部分QM和DE处于竖直向上的匀强磁场中，磁感应强度为B．a、b为材料相同、长都为L的导体棒，跨接在导轨上．已知a棒的质量为m、电阻为R，a棒的横截面是b的3倍．金属棒a和b都从距水平面高度为h的弧形导轨上由静止释放，分别通过DQ、EM同时进入匀强磁场中，a、b棒在水平导轨上运动时不会相碰．若金属棒a、b与导轨接触良好，且不计导轨的电阻和棒与导轨的摩擦．
（1）金属棒a、b刚进入磁场时，回路中感应电流的方向如何？
（2）通过分析计算说明，从金属棒a、b进入磁场至某金属第一次离开磁场的过程中，电路中产生的焦耳热．

Answer 1

分析：（1）根据楞次定律判断回路中感应电流的方向．
（2）分析两金属棒的运动情况：金属棒a、b同时进入磁场区域后，产生感应电流，受到安培力作用，速度都将发生变化，当a、b棒速度相同时，回路中磁通量不发生变化，不产生感应电流，不受安培力作用，金属棒a、b将共同匀速运动．a、b棒在水平方向所受合外力为零，类似于非弹性碰撞，根据动量守恒定律求出共同速度，由能量守恒求焦耳热．

解答：解：（1）根据楞次定律可判断出，金属棒a、b刚进入磁场时，回路中感应电流的方向为：QDEMQ．　
（2）金属棒从弧形轨道滑下，机械能守恒得：
由：mgh=

1

2

mv12
解出：v1=

2gh

金属棒a、b同时进入磁场区域后，产生感应电流，受到安培力作用，速度发生变化，当a、b棒同速时，回路中磁通量不发生变化，则不产生感应电流，不受安培力作用，金属棒a、b将共同匀速运动．　
由于a、b棒在水平方向所受合外力为零，故动量守恒，且由题可知：m_a=3m_b
有：m_av₁-m_bv₁=（m_a+m_b）v₂
解得：v2=

1

2

2gh

方向：水平向右．
所以金属棒a、b将以速度v₂匀速运动．　　
从金属棒a、b进入磁场开始，到金属棒b第一次离开磁场的过程中，系统总能量守恒，由：
  (ma+mb)gh=

1

2

(ma+mb)v22+Q
解出此过程中电路中产生的焦耳热：Q=mgh　
答：
（1）金属棒a、b刚进入磁场时，回路中感应电流的方向为：QDEMQ．
（2）电路中产生的焦耳热为mgh．

点评：该题考查了多个知识点的综合运用．做这类问题我们还是应该从运动过程和受力分析入手研究，运用一些物理规律求解问题．能量的转化与守恒的应用非常广泛，我们应该首先考虑．