题目内容
 如图所示,一束截面为圆形(半径R=1m)的平行紫光垂直射向一半径也为R的玻璃半球的平面,经折射后在屏幕S上形成一个圆形亮区.屏幕S至球心距离为D=(
如图所示,一束截面为圆形(半径R=1m)的平行紫光垂直射向一半径也为R的玻璃半球的平面,经折射后在屏幕S上形成一个圆形亮区.屏幕S至球心距离为D=(| 2 |
①若玻璃半球对紫色光的折射率为n=
| 2 |
②若将题干中紫光改为白光,在屏幕S上形成的圆形亮区的边缘是什么颜色?
分析:(1)光线沿直线从O点穿过玻璃,方向不变.从A点射出玻璃砖的光线方向向右偏折,射到屏幕S上圆形亮区,作出光路图,由光的折射定律结合数学几何知识求出圆形亮区的半径.
(2)当光线从空气垂直射入半圆玻璃砖,光线不发生改变,当入射角小于临界角时,光线才能再从玻璃砖射出,所以平行白光中的折射率不同,导致临界角不同,因此偏折程度不同,从而确定圆形亮区的最外侧的颜色;
(2)当光线从空气垂直射入半圆玻璃砖,光线不发生改变,当入射角小于临界角时,光线才能再从玻璃砖射出,所以平行白光中的折射率不同,导致临界角不同,因此偏折程度不同,从而确定圆形亮区的最外侧的颜色;
解答: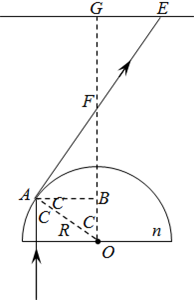 解:(1)如图,紫光刚要发生全反射时的临界光线射在屏幕S上的点E到亮区中心G的距离r就是所求最大半径.设紫光临界角为C,
解:(1)如图,紫光刚要发生全反射时的临界光线射在屏幕S上的点E到亮区中心G的距离r就是所求最大半径.设紫光临界角为C,
由全反射的知识得:sinC=
,
又:AB=RsinC=
,
OB=RcosC=R
,BF=AB?tanC=
,GF=D-(OB+BF)=D-
,
=
所以有r=GE=
?AB=D?
-nR=(
+1)
-
×1=1m
(2)紫色.当平行光从玻璃中射向空气时,由于紫光的折射率的最大,则临界角最小,所以首先发生全反射,因此出射光线与屏幕的交点最远.故圆形亮区的最外侧是紫光.
答:(1)若玻璃半球对(1)中最外侧色光的折射率为n,圆形亮区的最大半径为1m.
(2)屏幕S上形成的圆形亮区的最外侧是紫光;
 解:(1)如图,紫光刚要发生全反射时的临界光线射在屏幕S上的点E到亮区中心G的距离r就是所求最大半径.设紫光临界角为C,
解:(1)如图,紫光刚要发生全反射时的临界光线射在屏幕S上的点E到亮区中心G的距离r就是所求最大半径.设紫光临界角为C,由全反射的知识得:sinC=
| 1 |
| n |
又:AB=RsinC=
| R |
| n |
OB=RcosC=R
| ||
| n |
| R | ||
n
|
| nR | ||
|
| GE |
| AB |
| GF |
| FB |
所以有r=GE=
| GF |
| FB |
| n2-1 |
| 2 |
|
| 2 |
(2)紫色.当平行光从玻璃中射向空气时,由于紫光的折射率的最大,则临界角最小,所以首先发生全反射,因此出射光线与屏幕的交点最远.故圆形亮区的最外侧是紫光.
答:(1)若玻璃半球对(1)中最外侧色光的折射率为n,圆形亮区的最大半径为1m.
(2)屏幕S上形成的圆形亮区的最外侧是紫光;
点评:本题考查光的折射.关键是作出光路图,根据几何知识求出入射角与折射角,知道折射率和临界角的关系,了解各种色光的波长和折射率的关系.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 (2006?深圳二模)如图所示,一束截面为圆形(半径R)的平行白光垂直射向一玻璃半球的平面,经折射后在屏幕S上形成一个圆形彩色亮区.已知玻璃半球的半径为R,屏幕S至球心的距离为D(D>4R),不考虑光的干涉和衍射,试问:
(2006?深圳二模)如图所示,一束截面为圆形(半径R)的平行白光垂直射向一玻璃半球的平面,经折射后在屏幕S上形成一个圆形彩色亮区.已知玻璃半球的半径为R,屏幕S至球心的距离为D(D>4R),不考虑光的干涉和衍射,试问: 如图所示,一束截面为圆形、半径为R的平行单色光,垂直射向一玻璃半球的上表面,经折射后在屏幕S上形成一个圆形亮区.已知玻璃半球的半径为R,屏幕S到球心的距离为d(d>3R),玻璃对该单色光的折射率为n,不考虑光的干涉和衍射,求屏幕上被照亮区域的半径.
如图所示,一束截面为圆形、半径为R的平行单色光,垂直射向一玻璃半球的上表面,经折射后在屏幕S上形成一个圆形亮区.已知玻璃半球的半径为R,屏幕S到球心的距离为d(d>3R),玻璃对该单色光的折射率为n,不考虑光的干涉和衍射,求屏幕上被照亮区域的半径. 如图所示,一束截面为圆形(半径R)的平行单色光垂直射向一玻璃半球的平面,经折射后在屏幕P上形成一个圆形亮区.已知玻璃半球的直径为d=0.1米,屏幕p至球心的距离为s=0.4米,不考虑光的干涉和衍射,若玻璃半球对单色光的折射率为n=
如图所示,一束截面为圆形(半径R)的平行单色光垂直射向一玻璃半球的平面,经折射后在屏幕P上形成一个圆形亮区.已知玻璃半球的直径为d=0.1米,屏幕p至球心的距离为s=0.4米,不考虑光的干涉和衍射,若玻璃半球对单色光的折射率为n=
