题目内容
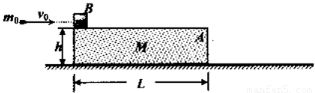
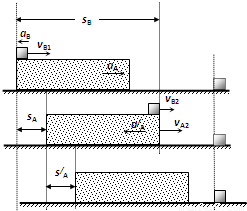
如图所示,一长度L=3m,高h=0.8m,质量为M=1kg的物块A静止在水平面上.质量为m=0.49kg的物块B静止在A的最左端,物块B与A相比大小可忽略不计,它们之间的动摩擦因数μ1=0.5,物块A与地之间的动摩擦因数μ2=0.1.-个质量为m=0.01kg可视为质点的子弹,以速度V沿水平方向射中物块B,假设在任何情况下子弹均不能穿出.g=1O/s2,问:(1 )子弹以v=400m/s击中物块B后的瞬间,它们的速度为多少?
(2 )被击中的物块B在A上滑动的过程中,A、B的加速度各为多少?
(3)子弹速度为多少时,能使物块B落地瞬间A同时停下?
【答案】分析:(1)子弹击中B过程中,由动量守恒定律求解
(2)对A、B受力分析,由牛顿第二定律求出加速度
(3)分析B在A上面滑动和B做平抛运动的过程,运用牛顿第二定律和运动学公式结合分析求解.
解答:解:(1)子弹击中B过程中,由动量守恒定律可得:
mv=(m+m)v
解得:v=8m/s
(2)由牛顿第二定律可得:
对B:μ1(m+m)g=(m+m)aB
aB=5m/s2,方向水平向左
对A:μ1(m+m)g-μ2(m+m+M)g=MaA
aA=1m/s2 向水平向右
(3)子弹击中B过程中,由动量守恒定律可得:
mv02=(m+m)vB1
设B在A上运动的时间为t1,
则:SB-SA=L
(vB1t1- aB
aB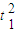 )-
)- aA
aA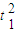 =L
=L
B做平抛运动时间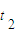 ,
,
h= gt2
gt2
a′A=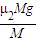 =1m/s2.
=1m/s2.
0=aAt1-a′At2
联立求解得:子弹速度v02=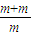 vm=435m/s
vm=435m/s
答:(1 )子弹以v=400m/s击中物块B后的瞬间,它们的速度是8m/s
(2 )被击中的物块B在A上滑动的过程中,A、B的加速度各为1m/s2和5m/s2,
(3)子弹速度为435m/s时,能使物块B落地瞬间A同时停下.
点评:解决该题关键要清楚物体的运动情况和受力情况,能把牛顿第二定律和运动学公式结合应用,同时运用到动量守恒定律.
(2)对A、B受力分析,由牛顿第二定律求出加速度
(3)分析B在A上面滑动和B做平抛运动的过程,运用牛顿第二定律和运动学公式结合分析求解.
解答:解:(1)子弹击中B过程中,由动量守恒定律可得:
mv=(m+m)v
解得:v=8m/s
(2)由牛顿第二定律可得:
对B:μ1(m+m)g=(m+m)aB
aB=5m/s2,方向水平向左
对A:μ1(m+m)g-μ2(m+m+M)g=MaA
aA=1m/s2 向水平向右
(3)子弹击中B过程中,由动量守恒定律可得:
mv02=(m+m)vB1
设B在A上运动的时间为t1,
则:SB-SA=L
(vB1t1-
 aB
aB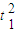 )-
)- aA
aA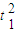 =L
=LB做平抛运动时间
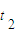 ,
,h=
 gt2
gt2a′A=
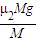 =1m/s2.
=1m/s2.0=aAt1-a′At2
联立求解得:子弹速度v02=
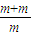 vm=435m/s
vm=435m/s
答:(1 )子弹以v=400m/s击中物块B后的瞬间,它们的速度是8m/s
(2 )被击中的物块B在A上滑动的过程中,A、B的加速度各为1m/s2和5m/s2,
(3)子弹速度为435m/s时,能使物块B落地瞬间A同时停下.
点评:解决该题关键要清楚物体的运动情况和受力情况,能把牛顿第二定律和运动学公式结合应用,同时运用到动量守恒定律.

练习册系列答案
相关题目
 (2012?深圳二模)如图所示,一长度L=3m,高h=0.8m,质量为M=1kg的物块A静止在水平面上.质量为m=0.49kg的物块B静止在A的最左端,物块B与A相比大小可忽略不计,它们之间的动摩擦因数μ1=0.5,物块A与地之间的动摩擦因数μ2=0.1.-个质量为m0=0.01kg可视为质点的子弹,以速度V0沿水平方向射中物块B,假设在任何情况下子弹均不能穿出.g=1O/s2,问:
(2012?深圳二模)如图所示,一长度L=3m,高h=0.8m,质量为M=1kg的物块A静止在水平面上.质量为m=0.49kg的物块B静止在A的最左端,物块B与A相比大小可忽略不计,它们之间的动摩擦因数μ1=0.5,物块A与地之间的动摩擦因数μ2=0.1.-个质量为m0=0.01kg可视为质点的子弹,以速度V0沿水平方向射中物块B,假设在任何情况下子弹均不能穿出.g=1O/s2,问: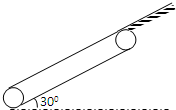 传送带现已广泛应用于机场、商店等公共场所,为人们的生活带来了很多的便利.如图所示,一长度L=7m的传送带与水平方向间的夹角α=30°,在电动机带动下以v=2m/s的速率顺时针匀速转动.在传送带上端接有一个斜面,斜面表面与传送带表面都在同一平面内.将质量m=2kg可视作质点的物体无初速地放在传送带底端,物体经传送带作用后能到达斜面顶端且速度为零.若物体与传送带及物体与斜面间的动摩擦因数都为μ=
传送带现已广泛应用于机场、商店等公共场所,为人们的生活带来了很多的便利.如图所示,一长度L=7m的传送带与水平方向间的夹角α=30°,在电动机带动下以v=2m/s的速率顺时针匀速转动.在传送带上端接有一个斜面,斜面表面与传送带表面都在同一平面内.将质量m=2kg可视作质点的物体无初速地放在传送带底端,物体经传送带作用后能到达斜面顶端且速度为零.若物体与传送带及物体与斜面间的动摩擦因数都为μ=