题目内容
14.如图1所示带斜面的足够长木板P,质量M=1kg.静止在水平地面上,其右侧靠竖直墙壁,倾斜面BC与水平面AB的夹角θ=37°,两者平滑对接.t=0s时,质量m=2kg、可视为质点的滑块Q从顶点C由静止开始下滑,图2所示为Q在O~6s内的速率v随时间t变化的部分图线.已知P与Q间的动摩擦因数μ1是P与地面间的动摩擦因数μ2的3倍,sin37°=0.6,cos37°=0.8,g取10m/s2.求: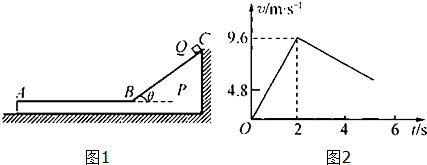
(1)物块Q与木板P间的动摩擦因数
(2)整个过程中木板P的最大速度大小.
分析 根据乙图可知,0-2s内物体做匀加速直线运动,2-6s内做匀减速直线运动,所以0-2s内在斜面上下滑,2-6s内在水平面上滑行,根据v-t图象求出加速度,再根据牛顿第二定律求出动摩擦力因数,进而求出木板P与地面间的动摩擦因数;分别对Q和P运用牛顿第二定律及运动学基本公式求解木板P的最大速度.
解答 解:(1)设物块Q在斜面上运动时的加速度a1,由图象知:${a}_{1}=\frac{△v}{△t}=\frac{9.6}{2}=4.8m/{s}^{2}$
由牛顿第二定律得:mgsin37°-μ1mgcos37°=ma1
由以上两式可得:μ1=0.15
(2)当物块滑上AB部分后,物块P向左减速,设加速度为a2,则有:
a${\;}_{2}=\frac{{μ}_{1}mg}{m}$=μ1g=1.5m/s2
对P因μ1mg>μ2(M+m)g,故木板向左加速,设加速度为a3,
由牛顿第二定律可得:μ1mg-μ2(M+m)g=Ma3
故得a${\;}_{3}=1.5m/{s}^{2}$
设经时间t后二者速度相同,则就有:
v1-a2t=a3t
可得:t=3.2s
此时的速度为v=a3t=1.5×3.2=4.8m/s
二者速度相等后,因μ1>μ2,将一起减速
故P的最大速度vp=4.8m/s
答:(1)物块Q与木板P间的动摩擦因数 0.15
(2)整个过程中木板P的最大速度大小4.8m/s.
点评 本题抓哟考查了匀变速直线运动及其公式、图象牛顿运动定律、牛顿定律的应用,要求同学们能正确分析物体的运动情况,能根据图象求解加速度和位移,难度较大.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
15.关于做匀速圆周运动的物体,下列说法正确的是( )
| A. | 物体线速度的大小和方向都是不变的 | |
| B. | 物体受到的向心力的大小和方向都是不变的 | |
| C. | 物体受到的向心力就是物体受到的指向圆心的合力 | |
| D. | 物体加速度的大小和方向都是不变的 |
5.根据玻尔理论,氢原子核外电子能级图如图所示,下列说法中正确的是( )


| A. | 按照玻尔理论,E1=-13.6eV是电子处于基态的势能 | |
| B. | 按照玻尔理论,E1=-13.6eV是电子处于基态的势能和动能之和 | |
| C. | 按照玻尔理论,从n=4的一群电子跃迁到n=1时,能发出6中不同频率的光子 | |
| D. | 按照玻尔理论,从n=4的一群电子跃迁到n=1时,能发出3中不同频率的光子 |
6.发现万有引力定律和测出引力常量的科学家分别是( )
| A. | 牛顿、卡文迪许 | B. | 伽利略、卡文迪许 | C. | 开普勒、牛顿 | D. | 第谷、伽利略 |
3.一个直流电动机所加电压为U,电流为I,线圈内阻为R,当它工作时,下述说法中错误的是( )
| A. | 电动机的输入功率为IU | B. | 电动机的发热功率为I2R | ||
| C. | 电动机的输出功率为IU-I2R | D. | 电动机的功率可写作IU=I2R=$\frac{{U}^{2}}{R}$ |
4.以下说法正确的是( )
| A. | 晶体都具有确定的熔点 | |
| B. | 空气相对湿度大,就是空气中水蒸气含量高 | |
| C. | 物体从外界吸收热量,其内能不一定增加 | |
| D. | 空调机在制冷过程中,从室内吸收的热量等于向室外放出的热量 |

 如图所示,质量为mA=2kg的木块A静止在光滑水平面上.一质量为mB=1kg的木块B某一初速度v0=5m/s沿水平方向向右运动,与木块A碰撞后都向右运动.木块A与档板碰撞后立即反弹(木块A与挡板碰撞过程中无机械能损失).后来木块A、B同向运动,速度大小分别为0.9m/s、1.2m/s.求:
如图所示,质量为mA=2kg的木块A静止在光滑水平面上.一质量为mB=1kg的木块B某一初速度v0=5m/s沿水平方向向右运动,与木块A碰撞后都向右运动.木块A与档板碰撞后立即反弹(木块A与挡板碰撞过程中无机械能损失).后来木块A、B同向运动,速度大小分别为0.9m/s、1.2m/s.求: