题目内容
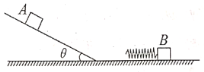
【题目】如图所示，一质量为m，电荷量为q（q>0）的小物块，在距离电场区域为a处以一定的初速度在一水平绝缘平面上向右运动，物块与绝缘平面的摩擦因数为
，物块在运动过程中要穿越宽度为2a，场强大小为E的电场区域，当场强方向竖直向下时，物块停留在离开电场区域左边缘的0.5a处，当场强方向向上时，物块停留在距离电场区域右侧的a处。求：
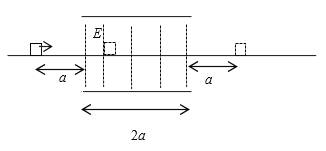
（1）电场强度的大小，以及物块的初速度;
（2）若增加物块初速度的大小，当电场向下时，物块仍能停在电场区域内。求电场向上时物块运动的时间与电场向下情况下物块运动时间差值的最小值。并求出对应的初速度。
【答案】（1）
；
（2）
；
【解析】
（1）当场强方向竖直向下时，由动能定理：
；
当场强方向竖直向上时，由动能定理：
；
联立解得： ；
（2）无论电场方向如何，物块在进入电场前运动时时间是相等的，设滑块刚进入电场时速度为v，当电场向下时物块不滑出电场，则由动量定理：
解得：
；
若场强向上，则由于mg=qE，则滑块在电场中受摩擦力为零而做匀速运动，出离电场后做运减速运动，则在电场中的时间为：
，
出离电场时：
，
则运动的总时间为：
；
则时间差：
；
由数学知识可知，当 
时，t最小，即当
时，t最小值为： ；
此时当场强向下时，有：
，解得x=a，滑块不滑出电场的范围；
由动能定理： 
，
解得： ；
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
