��Ŀ����
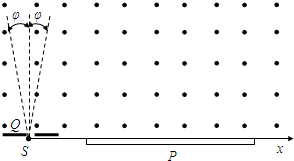 �������Dz�����������Ҫ�����������ǵĹ���ԭ����ͼ��ʾ������ԴS��������Ϊm������Ϊq�Ħ������ش�ֱ�ų��������Ÿ�Ӧǿ��ΪB����ǿ�ų�������������Q������2�յ�С�Ƕ��ڣ������Ӿ��ų�ƫת�����������ƽ�еĸй�ƬP�ϣ�������Ӱ�첻�ƣ�
�������Dz�����������Ҫ�����������ǵĹ���ԭ����ͼ��ʾ������ԴS��������Ϊm������Ϊq�Ħ������ش�ֱ�ų��������Ÿ�Ӧǿ��ΪB����ǿ�ų�������������Q������2�յ�С�Ƕ��ڣ������Ӿ��ų�ƫת�����������ƽ�еĸй�ƬP�ϣ�������Ӱ�첻�ƣ���1����������E��E+��E����E��0���ҡ�E?E����Χ�ڵĦ����Ӿ���ֱ�����������ķ������ų���������Щ�����Ӵ��ڽ�Ƭ�ϵķ�Χ��x1��
��2��ʵ���ϣ�����������һ���Ŀ��ȣ������ӽ���2�ս��ڽ���ų�������������ΪE�Ħ� ���Ӵй⽺Ƭ�ϵķ�Χ��x2��
��������1��������Բ���˶�����ֱ����պ�Ϊ��Բ����qvb=
��E=
mv2�����x�ı���ʽ���ֱ����E���E����ʽƽ������������ԡ�E2���x2�Ķ��η������������ʣ�
��2���ɼ��ι�ϵ��������ӱ߾����ߦս��������Ӵ���2Rcos�ճ����м��������Ӵ���2R����
| mv2 |
| R |
| 1 |
| 2 |
��2���ɼ��ι�ϵ��������ӱ߾����ߦս��������Ӵ���2Rcos�ճ����м��������Ӵ���2R����
�������������������ٶ�v����ų������ڽ�Ƭ�ϵ�λ�þ�S�ľ���Ϊx
Բ���˶� qvB=m
�����ӵĶ��� E=
mv2
�� x=2R
��ã�x=
��
��x1=
-
��x����1ʱ����1+x��n��1+xn
����ʽ�ɵã���x1��
��E��
��2������ΪE�Ħ������ء��ս����䣬����뾶��ͬ����ΪR
Բ���˶� qvB=m
�����ӵĶ��� E=
mv2
�ɼ��ι�ϵ�� ��x2=2R-2Rcos��=
(1-cos��)=
sin2

�𣺣�1����x1��
��E ��2����x2=
sin2
Բ���˶� qvB=m
| v2 |
| R |
�����ӵĶ��� E=
| 1 |
| 2 |
�� x=2R
��ã�x=
2
| ||
| qB |
��x1=
2
| ||
| Bq |
2
| ||
| Bq |
��x����1ʱ����1+x��n��1+xn
����ʽ�ɵã���x1��
| ||
| qBE |
��2������ΪE�Ħ������ء��ս����䣬����뾶��ͬ����ΪR
Բ���˶� qvB=m
| v2 |
| R |
�����ӵĶ��� E=
| 1 |
| 2 |
�ɼ��ι�ϵ�� ��x2=2R-2Rcos��=
2
| ||
| qB |
4
| ||
| qB |
| �� |
| 2 |

�𣺣�1����x1��
| ||
| qBE |
4
| ||
| qB |
| �� |
| 2 |
������������ҪӦ�ü���֪ʶ���Ӵ��˽���ų�������Ѷȣ���Ҫ����������ϰ���������ɣ�

��ϰ��ϵ�д�
�����Ŀ
 ���ڣ������Ӿ��ų�ƫת�����������ƽ�еĸй�ƬP�ϡ�������Ӱ�첻�ƣ�
���ڣ������Ӿ��ų�ƫת�����������ƽ�еĸй�ƬP�ϡ�������Ӱ�첻�ƣ� ͼ��ʾ������ԴS��������Ϊm������Ϊq���������ش�ֱ�ų��������Ÿ�Ӧǿ��ΪB����ǿ�ų�������������Q������2����С�Ƕ��ڣ������Ӿ��ų�ƫת�����������ƽ�еĸй�ƬP�ϡ�������Ӱ�첻�ƣ�
ͼ��ʾ������ԴS��������Ϊm������Ϊq���������ش�ֱ�ų��������Ÿ�Ӧǿ��ΪB����ǿ�ų�������������Q������2����С�Ƕ��ڣ������Ӿ��ų�ƫת�����������ƽ�еĸй�ƬP�ϡ�������Ӱ�첻�ƣ� �������Dz���
�������Dz���