题目内容
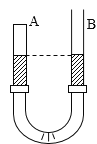
【题目】如图，平行板电容器两极间加上电压U，一质量为m、带正电荷量为q的粒子，从两极板正中间的M点由静止释放，粒子被电场加速，从下极板正对M点的小孔N飞出；在电容器的下方，有一个边长为L的正方体绝缘空腔，其截面如图，正方体的上边中点正对N孔也开有一小孔P，粒子从电容器飞出后恰好垂直上边从P飞入正方体空腔，整个空腔处在有上边界的垂直纸面向里的匀强磁场中；若粒子在正方体空腔中与四壁的碰撞都是弹性正碰（垂直四壁碰撞且碰撞前后速度大小相等、方向相反），且电荷量不变，粒子与空腔四壁除碰撞外无其他相互作用，粒子最终又从P点飞出空腔。不计粒子的重力和阻力，不计碰撞时间，求：
（1）粒子飞入空腔时的速度v0是多大？
（2）若v0为已知，则粒子在空腔中与四壁碰撞次数最少时运动的时间t0是多少？对应的磁感应强度B0是多大？
（3）若v0为已知，求所有满足条件的磁感应强度的大小，并计算对应的在空腔内运动的时间。
【答案】（1）
； （2）
；
【解析】试题分析：粒子被电场加速，由动能定理即可求出加速后的速度；粒子与另外三壁各碰一次且碰撞位置为各边中点时，碰撞次数最少，根据几何关系求出半径和时间，根据牛顿第二定律求出对应的磁感应强度；当粒子的半径应满足的关系式为：
（n=0，1，2…）时，由洛伦兹力提供向心力求出磁感应强度的大小和对应的在空腔内运动的时间。
（1）粒子被电场加速，由动能定理得：
解得：
（2）粒子与另外三壁各碰一次且碰撞位置为各边中点时，如图所示：碰撞次数最少
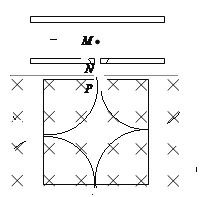
则运动半径为有：
，
可得：
在磁场中做匀速圆周运动，根据牛顿第二定律：
解得：
（3）粒子的半径应满足的关系式为： （n=0，1，2…）
所以：
由洛伦兹力提供向心力：
联立可得：
（n=0，1，2…）
则运动时间为：
（n=0,1,2…）
