题目内容
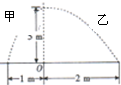
17. 如图所示,一列简谐横波沿x轴正方向传播,在t1=0和t2=0.05s的时刻,波的图象分别如图中的实线和虚线所示.求这列波的波速.
如图所示,一列简谐横波沿x轴正方向传播,在t1=0和t2=0.05s的时刻,波的图象分别如图中的实线和虚线所示.求这列波的波速.
分析 根据波形的平移法,结合波的周期性,得出波传播的距离与波长的关系,求得传播距离的通项,再由v=$\frac{x}{t}$求解波速通项.
解答 解:波沿x轴正方向传播:波传播的距离为x=(n+$\frac{1}{4}$)λ (m) (n=0,1,2,3,…)
则波速为v=$\frac{x}{t}=\frac{λ(4n+1)}{4t}=\frac{16(4n+1)}{4×0.05}$m/s=80(4n+1)m/s (n=0,1,2,3,…)
答:这列波的波速为v=80(4n+1)m/s(n=0,1,2,3,…).
点评 本题关键是根据波形的平移法确定波传播距离与波长的关系,难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.一摆长为L的单摆悬于O点,在O点正下方O′处钉一个光滑钉,使$\overline{OO'}$=$\frac{L}{2}$,将单摆拉开后释放,偏角总小于5°,此摆的周期为( )
| A. | 2π$\sqrt{\frac{L}{g}}$ | B. | 2π$\sqrt{\frac{L}{2g}}$ | C. | 2π($\sqrt{\frac{L}{g}}$+$\sqrt{\frac{L}{2g}}$) | D. | π($\sqrt{\frac{L}{g}}$+$\sqrt{\frac{L}{2g}}$) |
12.光在某种介质中传播的速度为1.5×108m/s,那么,光从此介质射向空气并发生全反射的临界角应为( )
| A. | 60° | B. | 45° | C. | 30° | D. | 75° |
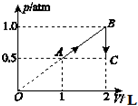 如图所示,一定质量的理想气体从状态A变化到状态B,再由状态B变化到状态C.已知状态A的温度为300K.1atm=1.0×105Pa
如图所示,一定质量的理想气体从状态A变化到状态B,再由状态B变化到状态C.已知状态A的温度为300K.1atm=1.0×105Pa



 如图所示,有电流I流过长方体金属块,金属块宽度为d,高为b,有一磁感应强度为B的匀强磁场垂直纸面向里,金属块单位体积内的自由电子数为n,电子的电量为e,则金属块上表面的电势比下表面的电势要低(填“高”或“低”),金属块上下表面间的电势差是$\frac{IB}{ned}$.
如图所示,有电流I流过长方体金属块,金属块宽度为d,高为b,有一磁感应强度为B的匀强磁场垂直纸面向里,金属块单位体积内的自由电子数为n,电子的电量为e,则金属块上表面的电势比下表面的电势要低(填“高”或“低”),金属块上下表面间的电势差是$\frac{IB}{ned}$. 横截面积为S,气缸固定不动.一条细线左端连接在活塞上,另一端跨过定滑轮后连接在一个质量为m的小桶,活塞静止不动,气缸外大气压强为p0.现缓慢向小桶中添加细沙,使活塞向右移动(活塞始终未被拉出气缸),当气缸的体积变成原来的1.5倍时,求所加细沙的质量.
横截面积为S,气缸固定不动.一条细线左端连接在活塞上,另一端跨过定滑轮后连接在一个质量为m的小桶,活塞静止不动,气缸外大气压强为p0.现缓慢向小桶中添加细沙,使活塞向右移动(活塞始终未被拉出气缸),当气缸的体积变成原来的1.5倍时,求所加细沙的质量.