题目内容
6．
如图所示，质量均为M的两个梯形木块A、B在水平力F的作用下，一起沿光滑的水平面运动，A与B的接触面光滑，且与水平面的夹角为37°，已知重力加速度为g，则要使A与B保持相对静止一起运动，水平力F最大为多少？
分析 隔离对B分析，抓住临界情况，即地面对N的支持力为零，根据牛顿第二定律B的最大加速度，再对整体根据牛顿第二定律求出F的最大值．
解答 解：当F最大时，地面对B的支持力为零，根据牛顿第二定律有：
Ncos37°=Mg，
解得：N=$\frac{5}{4}Mg$，
则B的最大加速度a=$\frac{Nsin37°}{M}=\frac{3}{4}g$
对整体，根据牛顿第二定律得：
F=2Ma=1.5Mg
即F的最大值为1.5Mg．
答：要使A与B保持相对静止一起运动，水平力F最大为1.5Mg．
点评 解决本题的关键抓住临界情况，即地面对B的支持力为零，结合牛顿第二定律，运用整体法和隔离法进行求解．
练习册系列答案
相关题目
5．
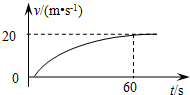如图所示为一辆汽车从静止开始运动的v-t图象，汽车达到的最大速度（匀速运动时的速度）为20m/s，设所用的时间为60s，则下列说法正确的是（ ）
如图所示为一辆汽车从静止开始运动的v-t图象，汽车达到的最大速度（匀速运动时的速度）为20m/s，设所用的时间为60s，则下列说法正确的是（ ）| A． | 汽车在这60s内的平均速度大于10m/s | |
| B． | 汽车在这60s内的加速度逐渐增大 | |
| C． | 汽车在这60s内的平均速度为10m/s | |
| D． | 汽车在这60s内的路程为600m |
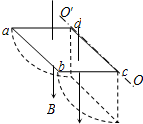可绕固定轴OO′转动的正方形线框的边长为L，不计摩擦和空气阻力，线框从水平位置由静止释放，达到竖直位置用的时间为t，ab边的速率为v，设线框始终处在方向竖直向下，磁感应强度为B的匀强磁场中，如图所示，求：
如图所示，在以2m/s2的加速度匀加速上升的升降机里，对紧贴厢壁质量为1kg的物体施加一水平力F，物体与厢壁的动摩擦因数μ=0.2，要使物体相对壁静止，求F的最小值（g取10m/s2）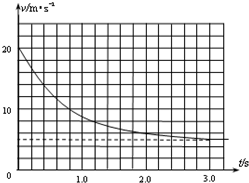
一般来说，正常人从距地面1.5m高处跳下，落地时速度较小，经过腿部的缓冲，这个速度对人是安全的，称为安全着地速度．如果人从高空跳下，必须使用降落伞才能安全着陆，其原因是，张开的降落伞受到空气对伞向上的阻力作用．经过大量实验和理论研究表明，空气对降落伞的阻力f与空气密度ρ、降落伞的迎风面积S、降落伞相对空气速度v、阻力系数c有关（由伞的形状、结构、材料等决定），其表达式是f=$\frac{1}{2}cρS{v^2}$．根据以上信息，解决下列问题．（取g=10m/s2）
11．关于物体带电，下列说法正确的是（ ）
| A． | 物体带正电或负电是物体缺少或多余电子的结果 | |
| B． | 物体不带电，是物体内没有电荷的结果 | |
| C． | 物体带正电，是别的物体正电荷转移到该物体身上的结果 | |
| D． | 以上说法都不对 |
15．如图所示，将小球沿与水平方向成α角，以速度v向右侧抛出，经时间t1击中墙上距水平面高度为h1的A点，再将此球从同一点以相同速度抛出，抛出速度与水平方向成β角（β＞ɑ），经时间t2击中墙上距水平面高度为h2的B点（图中为标出），空气阻力不计，则（ ）
| A． | t1不一定小于t2 | B． | 速度变化量，△v1可能大于△v2 | ||
| C． | h1一定小于h2 | D． | 重力做功W1可能大于W2 |
16．
如图所示，一个闭合三角形导线框ABC位于竖直平面内，其下方（略靠前）固定一根与线框平面平行的水平直线导线，导线中通过图示方向的恒定电流，释放线框，它由实线位置下落到虚线位置未发生转动，在此过程中穿过线框的磁通量（ ）
如图所示，一个闭合三角形导线框ABC位于竖直平面内，其下方（略靠前）固定一根与线框平面平行的水平直线导线，导线中通过图示方向的恒定电流，释放线框，它由实线位置下落到虚线位置未发生转动，在此过程中穿过线框的磁通量（ ）| A． | 逐渐增大 | |
| B． | 逐渐减小 | |
| C． | 始终为零 | |
| D． | 先增大，然后减小；在增大，最后又减小 |