题目内容
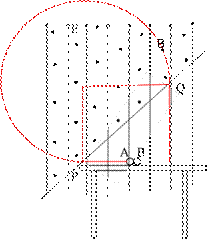
如图所示，整个空间中存在竖直向上的匀强电场。经过桌边的虚线PQ与桌面成45°角，其上方有足够大的垂直纸面向外的匀强磁场，磁感应强度为B。光滑绝缘水平桌面上有两个可以视为质点的绝缘小球，A球对桌面的压力为零，其质量为
，电量为q；B球不带电且质量为是km（k>7）。A、B间夹着质量可忽略的火药。现点燃火药（此时间极短且不会影响小球的质量、电量和各表面的光滑程度），火药炸完瞬间A的速度为
。求：
（1）火药爆炸过程中有多少化学能转化为机械能；
（2）A球在磁场中的运动时间；
（3）若一段时间后AB在桌上相遇，求爆炸前A球与桌边P的距离。
解析：（1）设爆炸之后B的速度为vB，选向左为正方向
在爆炸前后由动量守恒可得：
（2分）
又由能量守恒可得：
（2分）
（2）由“A球对桌面的压力为零”可知重力和电场力等大反向
故A球进入电场中将会做匀速圆周运动，则
（2分）
有几何知识可得：粒子在磁场中运动了
个圆周（2分）
则
（2分）
（3） 由可得：
（1分）
（1分）
设爆炸前A球与桌边P的距离为xA，爆炸后B运动的位移为xB，时间为tB
则
（2分）
（2分）
由图可得：
（2分）
联立上述各式解得：
（2分）
练习册系列答案
相关题目
如图所示，整个空间存在着水平向左电场强度E=5×102V/m的匀强电场，质量为M=2kg的小车B静止在光滑水平面上，现将一个质量为m=0.5kg带正电荷q=10-3C的小物体A无初速度放在B的右端，同时给小车B一个水平向右的恒力F=1N，它们将由静止开始运动．物体与小车之间绝缘且有摩擦力作用，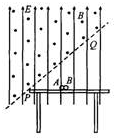
如图所示，整个空间中存在竖直向上的匀强电场．经过桌边的虚线PQ与桌面成45°角，其上方有足够大的垂直纸面向外的匀强磁场，磁感应强度为B．光滑绝缘水平桌面上有两个可以视为质点的绝缘小球，A球对桌面的压力为零，其质量为m，电量为q；B球不带电且质量为是km（k＞7）．A、B间夹着质量可忽略的火药．现点燃火药（此时间极短且不会影响小球的质量、电量和各表面的光滑程度），火药炸完瞬间A的速度为v0．求：
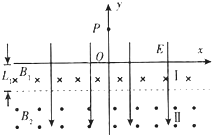如图所示，整个空间中存在竖直方向的匀强电场，场强大小E=10V/m，在x 轴下方存在两个相邻的匀强磁场区域Ⅰ、Ⅱ，磁场区域Ⅰ的宽度L1=12cm，磁感应强度B1=1.0T，方向垂直纸面向里，磁场区域Ⅱ的磁场方向垂直纸面向外．质量为m=10g电荷量为q=0.01C的带正电微粒在y轴上P点由静止释放，经过一段时间，进入磁场区域Ⅰ．通过控制装置，使质点每次通过x轴时，都使电场反向一次，但电场强度的大小不变．带电微粒在磁场区域Ⅰ中，速度方向改变37°时，进入磁场区域Ⅱ．已知sin37°=0.6，cos37°=0.8，g=10m/s2．