题目内容
15. 如图所示,皮带在轮O1O2带动下以速度v匀速转动,皮带与轮之间不打滑.皮带AB段长为L,皮带轮左端B处有一光滑小圆弧与一光滑斜面相连接.物体无初速放上皮带右端后,能在皮带带动下向左运动,并滑上斜面.已知物体与皮带间的动摩擦因数为μ,且μ>$\frac{{v}^{2}}{2gL}$.求:
如图所示,皮带在轮O1O2带动下以速度v匀速转动,皮带与轮之间不打滑.皮带AB段长为L,皮带轮左端B处有一光滑小圆弧与一光滑斜面相连接.物体无初速放上皮带右端后,能在皮带带动下向左运动,并滑上斜面.已知物体与皮带间的动摩擦因数为μ,且μ>$\frac{{v}^{2}}{2gL}$.求:(1)若物体无初速放上皮带的右端A处,则其运动到左端B处的时间.
(2)若物体无初速地放到皮带上某处,物体沿斜面上升到最高点后沿斜面返回,问物体滑回皮带后,是否有可能从皮带轮的右端A处滑出?判断并说明理由.
分析 (1)物块滑上传送带先做匀加速直线运动,当达到传送带速度时,一起做匀速直线运动,求出匀加速直线运动和匀速直线运动的时间之和,即为物体从右端滑到左端的时间.
(2)物块从斜面返回皮带的速度与物体滑上斜面的初速度大小相等,无初速放到皮带上某处,可能先做匀加速后做匀速,也可能一直做匀加速达不到传送带的速度,所以返回时最远不能超过释放的初始位置.
解答 解:(1)物体放上皮带运动的加速度 a=μg
物体加速到v前进的位移 x0=$\frac{{v}^{2}}{2a}$=$\frac{{v}^{2}}{2μg}$
因L>x0,则物体先加速后匀速,加速时间 t1=$\frac{v}{a}$=$\frac{v}{μg}$
匀速时间 t2=$\frac{L-{x}_{0}}{v}$=$\frac{L}{v}$-$\frac{v}{2μg}$
故物体从A到B时间 t=t1+t2=$\frac{L}{v}$+$\frac{v}{2μg}$
(2)不能滑出右端A.
理由:物体从斜面返回皮带的速度与物体滑上斜面的初速度大小相等,所以返回时最远不能超过释放的初始位置.
答:
(1)若物体无初速放上皮带的右端A处,则其运动到左端B处的时间是$\frac{L}{v}$+$\frac{v}{2μg}$.
(2)不能滑出右端A.理由:物体从斜面返回皮带的速度与物体滑上斜面的初速度大小相等,所以返回时最远不能超过释放的初始位置.
点评 解决本题的关键根据物块的受力,判断物体的运动状况,加速度是联系前后的桥梁.

练习册系列答案
相关题目
5.在《用打点计时器测速度》实验中,
(1)需要的器材有:打点计时器、长木板、复写纸片、6v低压交变电源、纸带、刻度尺、导线.
(2)下列说法正确的是B
A.拖动纸带的同时,闭合电源开关
B.先闭合电源开关,让打点计时器正常工作时,拖动纸带
C.纸带上的打点密集说明纸带运动速度较大
D.利用打出的纸带可以准确的求出打下某些点时纸带运动的瞬时速度
(3)某同学拖动纸带运动,打点计时器在纸带上打出一系列点,处理时每隔1个点取一个记数点,标上字母A、B、C、D、E、F.
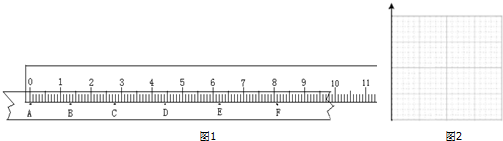
如图1所示,某同学用mm刻度尺进行测量,请帮忙读出B、C、D、E、F在刻度尺上的位置,填到表中:
由读出数据可计算出打下AF段纸带时小车的平均速度为4.05 m/s.
(4)若认为一段时间中间时刻的瞬时速度就是这段时间内的平均速度,则打点计时器打下C点时小车的速度VC=4.388m/s,小车从C点运动D点过程中的加速度a=1.00m/s2.
(5)在如图2所给坐标纸上建好坐标,作出纸带运动的打下B至E点的速度-时间图象(即v-t图象)(从打下A点开始计时).
(1)需要的器材有:打点计时器、长木板、复写纸片、6v低压交变电源、纸带、刻度尺、导线.
(2)下列说法正确的是B
A.拖动纸带的同时,闭合电源开关
B.先闭合电源开关,让打点计时器正常工作时,拖动纸带
C.纸带上的打点密集说明纸带运动速度较大
D.利用打出的纸带可以准确的求出打下某些点时纸带运动的瞬时速度
(3)某同学拖动纸带运动,打点计时器在纸带上打出一系列点,处理时每隔1个点取一个记数点,标上字母A、B、C、D、E、F.

如图1所示,某同学用mm刻度尺进行测量,请帮忙读出B、C、D、E、F在刻度尺上的位置,填到表中:
| 计数点 | B | C | D | E | F |
| 单位(cm) |
(4)若认为一段时间中间时刻的瞬时速度就是这段时间内的平均速度,则打点计时器打下C点时小车的速度VC=4.388m/s,小车从C点运动D点过程中的加速度a=1.00m/s2.
(5)在如图2所给坐标纸上建好坐标,作出纸带运动的打下B至E点的速度-时间图象(即v-t图象)(从打下A点开始计时).
3.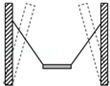 目前,我市每个社区均已配备了公共体育健身器材.图示器材为一秋千,用两根等长轻绳将一座椅悬挂在竖直支架上等高的两点.由于长期使用,导致两根支架向内发生了稍小倾斜,如图中虚线所示,但两悬挂点仍等高.座椅静止时单根轻绳对座椅拉力的大小,与倾斜前相比( )
目前,我市每个社区均已配备了公共体育健身器材.图示器材为一秋千,用两根等长轻绳将一座椅悬挂在竖直支架上等高的两点.由于长期使用,导致两根支架向内发生了稍小倾斜,如图中虚线所示,但两悬挂点仍等高.座椅静止时单根轻绳对座椅拉力的大小,与倾斜前相比( )
 目前,我市每个社区均已配备了公共体育健身器材.图示器材为一秋千,用两根等长轻绳将一座椅悬挂在竖直支架上等高的两点.由于长期使用,导致两根支架向内发生了稍小倾斜,如图中虚线所示,但两悬挂点仍等高.座椅静止时单根轻绳对座椅拉力的大小,与倾斜前相比( )
目前,我市每个社区均已配备了公共体育健身器材.图示器材为一秋千,用两根等长轻绳将一座椅悬挂在竖直支架上等高的两点.由于长期使用,导致两根支架向内发生了稍小倾斜,如图中虚线所示,但两悬挂点仍等高.座椅静止时单根轻绳对座椅拉力的大小,与倾斜前相比( )| A. | 变小 | B. | 变大 | C. | 不变 | D. | 无法确定 |
10.下列说法正确的( )
| A. | 放射性元素的半衰期与压力、温度无关 | |
| B. | 德布罗意认为一切物体都具有波粒二象性 | |
| C. | 处于n=3的一个氢原子回到基态时一定会辐射三种频率的光子 | |
| D. | 黑体辐射电磁波的强度按波长分布只与温度有关 |
7.某同学做“描绘小灯泡的伏安特性曲线”实验,实验室提供了表中的器材.

(1)为了使实验误差尽可能小,应选用的电流表是A1,电压表是V1.
(2)若该同学已正确选用器材,并连接好部分实验电路.如图1所示,请在图中完成其余的电路连接,要求小灯泡两端的电压能在 0~2.5V范围连续变化,且尽可能减少实验误差.实验开始时,滑动变阻器的滑片应该置于最左 端.(填“左”或“右”)
(3)该同学在正确完成实验后得到如图2所示的伏安特性曲线,他从图线中得到“通过小灯泡的电流随电压的增大而增大”的规律.请你分析图线再写出一条规律:小灯泡的电阻随温度的升高而增大.
| 小灯泡L(额定电压2.5V,额定电流250mA) | 直流电源E(电动势3V,内阻不计) |
| 电流表A1(量程300mA,内阻约0.5Ω) | 电流表A2(量程500mA,内阻约0.2Ω) |
| 电压表V1(量程3V,内阻约3kΩ) | 电压表V2(量程6V,内阻约6kΩ) |
| 滑动变阻器(最大阻值约10Ω) | 开关S,导线若干 |

(1)为了使实验误差尽可能小,应选用的电流表是A1,电压表是V1.
(2)若该同学已正确选用器材,并连接好部分实验电路.如图1所示,请在图中完成其余的电路连接,要求小灯泡两端的电压能在 0~2.5V范围连续变化,且尽可能减少实验误差.实验开始时,滑动变阻器的滑片应该置于最左 端.(填“左”或“右”)
(3)该同学在正确完成实验后得到如图2所示的伏安特性曲线,他从图线中得到“通过小灯泡的电流随电压的增大而增大”的规律.请你分析图线再写出一条规律:小灯泡的电阻随温度的升高而增大.
4. 如图甲所示为一列沿水平方向传播的简谐横波在某时刻t的波形图,其波速为200m/s,如图乙所示为质点b从时刻t开始计时的v-t图象.若设沿y轴方向为正方向,则下列说法中正确的是( )
如图甲所示为一列沿水平方向传播的简谐横波在某时刻t的波形图,其波速为200m/s,如图乙所示为质点b从时刻t开始计时的v-t图象.若设沿y轴方向为正方向,则下列说法中正确的是( )
 如图甲所示为一列沿水平方向传播的简谐横波在某时刻t的波形图,其波速为200m/s,如图乙所示为质点b从时刻t开始计时的v-t图象.若设沿y轴方向为正方向,则下列说法中正确的是( )
如图甲所示为一列沿水平方向传播的简谐横波在某时刻t的波形图,其波速为200m/s,如图乙所示为质点b从时刻t开始计时的v-t图象.若设沿y轴方向为正方向,则下列说法中正确的是( )| A. | 该简谐横波沿x轴正方向传播 | |
| B. | 在时刻t时,质点a的加速度方向沿y轴负向 | |
| C. | 若此波遇到另一简谐波并发生稳定干涉现象,则该波所遇到的波的频率为50 Hz | |
| D. | 若该波发生明显的衍射现象,则该波所遇到的障碍物的大小比4 m小或差不多 | |
| E. | 从t时刻计时开始,经过1s,质点a运动的路程为20m |
5.在“探究小车速度随时间变化的规律”实验中,下列说法正确的是( )
| A. | 先释放纸带,再接通电源 | |
| B. | 先接通电源,后释放纸带 | |
| C. | 纸带上打点越密集说明纸带运动速度越大 | |
| D. | 利用打出的纸带可以求出打下某点时纸带的瞬时速度 |

 某同学在做研究平抛物体运动规律的实验时得到了如图所示的小球的运动轨迹,A、B、C三点的位置在运动轨迹上已标出.其中A点的坐标为(0,0),g=10m/s2,则
某同学在做研究平抛物体运动规律的实验时得到了如图所示的小球的运动轨迹,A、B、C三点的位置在运动轨迹上已标出.其中A点的坐标为(0,0),g=10m/s2,则