题目内容
如图所示是计算机模拟出的一种宇宙空间的情境，在此宇宙空间存在这样一个远离其他空间的区域(其他星体对该区域内物体的引力忽略不计)，以MN为界，上半部分匀强磁场的磁感应强度为B1，下半部分匀强磁场的磁感应强度为B2。已知B1=4B2=4B0，磁场方向相同，且磁场区域足够大。在距离界线MN为h的P点有一宇航员处于静止状态，宇航员以平行于MN的速度向右抛出一质量为m、电荷量为q的带负电小球，发现小球在界线处的速度方向与界线成90°角，接着小球进入下半部分磁场。当宇航员沿与界线平行的直线匀速到达目标Q点时，刚好又接住球而静止。
(1)请你粗略地作出小球从P点运动到Q点的运动轨迹；
(2)PQ间的距离是多大?
(3)宇航员的质量是多少?
(1)小球的运动轨迹如下图所示
(2)设小球的速率为v1，由几何关系可知R1=h
由qvB=
和B1=4B2=4B0
可知R2=4R1=4h
由qv1(4B0)=
解得小球的速率v1=
根据运动的对称性，PQ的距离为L=2(R2-R1)=6h
(3)设宇航员的速率为v2，因周期T=2πR／v
故小球由P运动到Q的时间t=
所以宇航员匀速运动的速率为v2=
由动量守恒定律有Mv2-mv1=0
解得宇航员的质量M=
练习册系列答案
相关题目
（2007?东台市模拟）用计算机辅助实验系统（DIS）做验证牛顿第三定律的实验，如图所示是把两个测力探头的挂钩钩在一起，向相反方向拉动，观察显示器屏幕上出现的结果．观察分析两个力传感器的相互作用随着时间变化的曲线，以下结论的不正确的是（ ）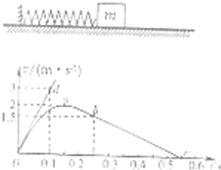
（2011?潍坊模拟）如图所示，水平地面上轻弹簧左端固定，右端通过滑块压缩0.4m锁定．t=0时解除锁定释放滑块．计算机通过滑块上的速度传感器描绘出滑块的速度图象如图所示，其中Oab段为曲线，bc段为直线，倾斜直线Od是t=0时的速度图线的切线，已知滑块质量m=10kg，取g=10m/s2，求：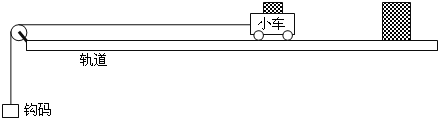
（2009?上海模拟）用DIS描绘电场等势线的实验中，在平整的木板上依次铺放白纸、复写纸和导电纸．在导电纸上平放两个圆柱形电极A与B，分别与直流电源的正、负极相连，如图所示．若以A、B连线为x轴，A、B连线的中垂线为y轴．将一个探针固定在y轴上的某一点，沿x轴移动另一个探针，发现无论怎样移动，计算机屏幕上电压测量值始终为零，若电源及连线都是完好的，可能的故障是