题目内容
9. 如图所示为皮带传动装置,左轮O1是一个轮轴,大轮半径为R1,小轮半径为R2,A、B分别是大轮和小轮边缘上的点,右轮O2的半径为R3,C是右轮边缘上的点,已知R1:R2:R3=3:2:1,转动中皮带不打滑.
如图所示为皮带传动装置,左轮O1是一个轮轴,大轮半径为R1,小轮半径为R2,A、B分别是大轮和小轮边缘上的点,右轮O2的半径为R3,C是右轮边缘上的点,已知R1:R2:R3=3:2:1,转动中皮带不打滑.(1)ωA:ωB=1:1,vA:vB=3:2
(2)ωA:ωC=1:3,vA:vC=1:1
(3)ωA:ωB:ωC=1:1:3,vA:vB:vC=3:2:3.
分析 对于A与C,由于皮带不打滑,线速度大小相等.对于B与A绕同一转轴转动,角速度相等,由v=ωr研究A与C的角速度关系,再根据a=ω2r求出向心加速度之比.
解答 解:(1)对于A与B,绕同一转轴转动,角速度相等,即ωA=ωB.由v=ωr和R1:R2=3:2,所以:vA:vB=R1:R2=3:2
(2)对于A与C,由于皮带不打滑,线速度大小相等,即vA=vC.由v=ωr得ωA:ωC=r3:r1=1:3.
(3)由以上的分析,则ωA:ωB:ωC=1:1:3,vA:vB:vC=3:2:3
故答案为:(1)1:1,3:2;(2)1:3,1:1;(3)1:1:3,3:2:3
点评 本题运用比例法解决物理问题的能力,关键抓住相等的量:对于不打滑皮带传动的两个轮子边缘上各点的线速度大小相等;同一轮上各点的角速度相同.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
19.如图所示,一物体以速度v0冲向光滑斜面AB,并能沿斜面升高h,下列说法正确的是( )
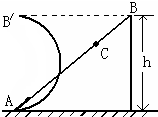

| A. | 若把斜面从C点锯断,由机械能守恒定律知,物体冲出C点后仍能升高h | |
| B. | 若把斜面弯成如图所示的半圆弧形,物体仍能沿AB升高h | |
| C. | 若把斜面从C点锯断或弯成如图所示的半圆弧状,物体都不能升高h,因为机械能不守恒 | |
| D. | 若把斜面从C点锯断或弯成如图所示的半圆弧状,物体都不能升高h,但机械能仍守恒 |
20.关于开普勒行星运动定律的应用,下面结论正确的是( )
| A. | 地球的所有卫星都绕地球在椭圆或圆轨道上运行,地球位于椭圆的一个焦点上或圆心上 | |
| B. | 地球的所有卫星与地心连线相等时间内扫过的面积相等 | |
| C. | 地球的所有卫星椭圆轨道半长轴的立方或圆轨道半径立方与卫星公转周期平方之比相等 | |
| D. | 开普勒行星运动定律只适用于行星绕太阳运动 |
14. (多选)如图,一长为L的轻质细杆一端与质量为m的小球(可视为质点)相连,另一端可绕O点转动,现使轻杆在同一竖直面内作匀速转动,测得小球的向心加速度大小为g(g为当地的重力加速度),下列说法正确的是( )
(多选)如图,一长为L的轻质细杆一端与质量为m的小球(可视为质点)相连,另一端可绕O点转动,现使轻杆在同一竖直面内作匀速转动,测得小球的向心加速度大小为g(g为当地的重力加速度),下列说法正确的是( )
 (多选)如图,一长为L的轻质细杆一端与质量为m的小球(可视为质点)相连,另一端可绕O点转动,现使轻杆在同一竖直面内作匀速转动,测得小球的向心加速度大小为g(g为当地的重力加速度),下列说法正确的是( )
(多选)如图,一长为L的轻质细杆一端与质量为m的小球(可视为质点)相连,另一端可绕O点转动,现使轻杆在同一竖直面内作匀速转动,测得小球的向心加速度大小为g(g为当地的重力加速度),下列说法正确的是( )| A. | 小球的线速度大小为gL | |
| B. | 小球运动到最高点时处于完全失重状态 | |
| C. | 当轻杆转到水平位置时,轻杆对小球作用力方向斜向上与半径成45°角 | |
| D. | 轻杆在匀速转动过程中,轻杆对小球作用力的最大值为mg |
1.某同学要测量一节旧电池的电动势和内阻,实验器材仅有一个电流表、一个电阻箱、一个开关和导线若干,该同学按如实图1所示电路进行实验,测得的数据如表所示.

(1)若利用图象确定电池的电动势和内阻,则应作R-$\frac{1}{I}$(填“R-I”或“R-$\frac{1}{I}$”)图象;
(2)利用测得的数据在实图2中画出适当的图象;
(3)由图象可知,该电池的电动势E=5.6V,内阻r=0.5Ω(保留到小数点后一位)
| 实验次数 | 1 | 2 | 3 | 4 | 5 |
| R(Ω) | 4.0 | 10.0 | 16.0 | 22.0 | 28.0 |
| I(A) | 1.00 | 0.50 | 0.34 | 0.25 | 0.20 |
| 1/I(A-1) | 1.0 | 2.0 | 2.9 | 4.0 | 5.0 |

(1)若利用图象确定电池的电动势和内阻,则应作R-$\frac{1}{I}$(填“R-I”或“R-$\frac{1}{I}$”)图象;
(2)利用测得的数据在实图2中画出适当的图象;
(3)由图象可知,该电池的电动势E=5.6V,内阻r=0.5Ω(保留到小数点后一位)
14.如图所示是某电磁冲击钻的原理图,若突然发现钻头M向右运动,则可能是( )
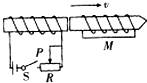

| A. | 电路突然出现断路 | |
| B. | 开关S由闭合到断开的瞬间 | |
| C. | 开关S已经是闭合的,滑动变阻器滑片P向左迅速滑动 | |
| D. | 开关S已经是闭合的,滑动变阻器滑片P向右迅速滑动 |
15. 如图我国女子短道速滑队在2013年世锦赛上实现女子3 000m接力三连冠.观察发现,“接棒”的运动员甲提前站在“交棒”的运动员乙前面,并且开始向前滑行,待乙追上甲时,乙猛推甲一把,使甲获得更大的速度向前冲出.在乙推甲的过程中,忽略运动员与冰面间在水平方向上的相互作用,则( )
如图我国女子短道速滑队在2013年世锦赛上实现女子3 000m接力三连冠.观察发现,“接棒”的运动员甲提前站在“交棒”的运动员乙前面,并且开始向前滑行,待乙追上甲时,乙猛推甲一把,使甲获得更大的速度向前冲出.在乙推甲的过程中,忽略运动员与冰面间在水平方向上的相互作用,则( )
 如图我国女子短道速滑队在2013年世锦赛上实现女子3 000m接力三连冠.观察发现,“接棒”的运动员甲提前站在“交棒”的运动员乙前面,并且开始向前滑行,待乙追上甲时,乙猛推甲一把,使甲获得更大的速度向前冲出.在乙推甲的过程中,忽略运动员与冰面间在水平方向上的相互作用,则( )
如图我国女子短道速滑队在2013年世锦赛上实现女子3 000m接力三连冠.观察发现,“接棒”的运动员甲提前站在“交棒”的运动员乙前面,并且开始向前滑行,待乙追上甲时,乙猛推甲一把,使甲获得更大的速度向前冲出.在乙推甲的过程中,忽略运动员与冰面间在水平方向上的相互作用,则( )| A. | 甲对乙的冲量一定与乙对甲的冲量相同 | |
| B. | 甲、乙的动量变化一定大小相等方向相反 | |
| C. | 甲的动能增加量一定等于乙的动能减少量 | |
| D. | 甲对乙做多少负功,乙对甲就一定做多少正功 |