题目内容
20. A、B、C、D是四块材料相同的木块,A、C的质量为m,B、D的质量为2m,水平面光滑,木块间的动摩擦因数为μ.在水平力F的作用下,四个木块始终一起运动,则在此过程中C、D间的摩擦力不会超过( )
A、B、C、D是四块材料相同的木块,A、C的质量为m,B、D的质量为2m,水平面光滑,木块间的动摩擦因数为μ.在水平力F的作用下,四个木块始终一起运动,则在此过程中C、D间的摩擦力不会超过( )| A. | μmg | B. | $\frac{2μmg}{3}$ | C. | $\frac{2μmg}{5}$ | D. | $\frac{μmg}{5}$ |
分析 根据摩擦定律知,AB间最大静摩擦力为μmAg,以BCD整体为研究对象可得整体所能获得的最大加速度,再以C为研究对象得出CD间的最大静摩擦力即可.
解答 解:由题意知,AB间最大静摩擦力fm=μmAg=μmg
则以BCD整体为研究对象可得,整体获得的最大加速度
${a}_{m}=\frac{{f}_{m}}{{m}_{C}+{m}_{B}+{m}_{D}}$=$\frac{μmg}{m+2m+2m}=\frac{μg}{5}$
再以C为研究对象可知,当BCD以最大加速度am运动时,CD间的摩擦力最大,此时
最大摩擦力${f}_{max}={m}_{C}{a}_{m}=m\frac{μg}{5}=\frac{μmg}{5}$
所以D正确,ABC错误.
故选:D.
点评 解决本题的关键是能根据整体法求得整体在摩擦力作用下获得的最大加速度,再根据隔离法求CD间的最大摩擦力,抓住加速度一致是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 我省举重运动员石智勇、张国政多次在世界级大赛中摘金夺银.在举重比赛中,运动员举起杠铃后保持稳定的一段时间,如图所示.下列说法中正确的是( )
我省举重运动员石智勇、张国政多次在世界级大赛中摘金夺银.在举重比赛中,运动员举起杠铃后保持稳定的一段时间,如图所示.下列说法中正确的是( )
 我省举重运动员石智勇、张国政多次在世界级大赛中摘金夺银.在举重比赛中,运动员举起杠铃后保持稳定的一段时间,如图所示.下列说法中正确的是( )
我省举重运动员石智勇、张国政多次在世界级大赛中摘金夺银.在举重比赛中,运动员举起杠铃后保持稳定的一段时间,如图所示.下列说法中正确的是( )| A. | 运动员对杠铃的作用力大于杠铃对运动员的作用力 | |
| B. | 运动员对杠铃的作用力小于杠铃对运动员的作用力 | |
| C. | 运动员对杠铃的作用力与杠铃对运动员的作用力是一对平衡力 | |
| D. | 运动员对杠铃的作用力与杠铃对运动员的作用力是一对作用力与反作用力 |
11.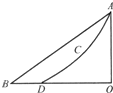 物体从某一高度由静止开始滑下,第一次经光滑斜面滑至底端时间为t1,第二次经过光滑曲面ACD滑至底端时间为t2,如图所示,设两次通过的路程相等,则t1与t2的大小关系是( )
物体从某一高度由静止开始滑下,第一次经光滑斜面滑至底端时间为t1,第二次经过光滑曲面ACD滑至底端时间为t2,如图所示,设两次通过的路程相等,则t1与t2的大小关系是( )
 物体从某一高度由静止开始滑下,第一次经光滑斜面滑至底端时间为t1,第二次经过光滑曲面ACD滑至底端时间为t2,如图所示,设两次通过的路程相等,则t1与t2的大小关系是( )
物体从某一高度由静止开始滑下,第一次经光滑斜面滑至底端时间为t1,第二次经过光滑曲面ACD滑至底端时间为t2,如图所示,设两次通过的路程相等,则t1与t2的大小关系是( )| A. | t2=t1 | B. | t2>t1 | C. | t1>t2 | D. | 无法确定 |
5. 如图所示,容器中盛有水,PM为水面,从A点发出一束白光,射到水面上的O点后,折射光发生了色散照到器壁上a、b之间,对应a、b两种颜色的单色光,则( )
如图所示,容器中盛有水,PM为水面,从A点发出一束白光,射到水面上的O点后,折射光发生了色散照到器壁上a、b之间,对应a、b两种颜色的单色光,则( )
 如图所示,容器中盛有水,PM为水面,从A点发出一束白光,射到水面上的O点后,折射光发生了色散照到器壁上a、b之间,对应a、b两种颜色的单色光,则( )
如图所示,容器中盛有水,PM为水面,从A点发出一束白光,射到水面上的O点后,折射光发生了色散照到器壁上a、b之间,对应a、b两种颜色的单色光,则( )| A. | 由A到O,a光的传播时间大于b光的传播时间 | |
| B. | 若发光点A不动而入射点O逐渐向右移动,则b光最先从器壁上消失 | |
| C. | 用a光和b光分别在同一套双缝干涉实验装置上做实验,a光的条纹间距较宽 | |
| D. | 用a光和b光分别照射同一金属都能发生光电效应,则a光产生的光电子的最大初动能大于b光产生的光电子的最大初动能 |
12.甲、乙、丙三图中物体的质量相同,弹簧秤、绳和滑轮的质量均不计,绳与滑轮间的摩擦力不计.在图甲、乙、丙中,弹簧秤的读数分别是F1、F2、F3,则( )

| A. | F3>F1=F2 | B. | F3=F1>F2 | C. | F1=F2=F3 | D. | F1>F2=F3 |
20.以下说法中不正确的是( )
| A. | 洛伦兹力可以对运动电荷做功 | |
| B. | 洛伦兹力可以改变运动电荷的速度大小 | |
| C. | 静止于磁场中的电荷可能受洛伦兹力 | |
| D. | 运动电荷在磁场中不一定受洛伦兹力 |

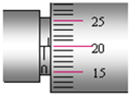 某同学在做测金属丝的电阻率的实验中,用螺旋测微器测量金属丝的直径如图所示,直径d=0.700mm.如测得金属丝的长度为L,直径为d,两端的电压为U,通过的电流为I,则金属丝的电阻率ρ=$\frac{πU{d}^{2}}{4IL}$(用题目给的物理量符号表达).
某同学在做测金属丝的电阻率的实验中,用螺旋测微器测量金属丝的直径如图所示,直径d=0.700mm.如测得金属丝的长度为L,直径为d,两端的电压为U,通过的电流为I,则金属丝的电阻率ρ=$\frac{πU{d}^{2}}{4IL}$(用题目给的物理量符号表达).