Question

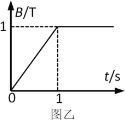
【题目】如图甲所示，在水平面上固定有长为L=2 m，宽为d=0.5 m的光滑金属“U”型导轨，导轨右端接有R1=2 Ω，R2=6 Ω的两个电阻，在“U”型导轨右侧l=1 m范围内存在垂直纸面向里的匀强磁场，且磁感应强度随时间变化规律如图乙所示。在t=0时刻．质量为m=0.1 kg，内阻r=0.5 Ω，导体棒ab以v0=2 m/s初速度从导轨的左端开始向口运动，导轨的电阻忽略不计，g取10 m/s2。求：

(1)第一秒内流过ab电流的大小及方向；

(2)第一秒内流过电阻R1的电荷量；

(3) ab电棒进入磁场瞬间的加速度大小及全过程回路中产生的焦耳热。

Answer 1

【答案】(1)0.25A由a流向b；(2)0.19C；(3) l. 25m/s2，0.175 J。

【解析】

(1)第一秒内磁场随时间均匀变化，由法拉第电磁感应定律有：

E1===0.5V，

所以流过ab的电流 ：

，

方向：由a流向b。

(2) 由闭合电路欧姆定律可得，第一秒电阻R1的两端的电压为：

则第一秒流过电阻R1的电流：

第一秒内流过电阻R1的电荷量

(3)依题意可知ab棒在1 s末时刻进入磁场(速度仍为v0)，此后磁感应强度保持不变，则

E2=Bdv0=0.5V，

I2== 0.25A，

安培力为：F=BI2d

由牛顿第二定律，有BI2d =ma，

联立可得：

a=l.25m/s2；

根据焦耳定律可得：

Q1=I(R+r)t1=0.125J，

Q2=mv=0.05J，

全过程回路产生的焦耳热：

Q= Q1+ Q2=0.175J；