题目内容
【题目】如图所示,一半径R=0.4 m的圆盘水平放置,绕竖直轴OO′匀速转动,在圆盘上方h=0.8 m处有一水平轨道,O′点左侧x0=2 m处有一质量m=1 kg的小球在F=4.25 N的水平恒力作用下由静止开始运动,当小球运动到O′点时撤走外力F,小球从O′点离开轨道,此时圆盘半径OA恰与小球的速度平行,且OA与速度都沿x轴正方向,g取10 m/s2。为了保证小球刚好落在A点,则:
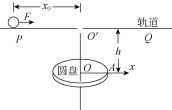
(1)小球与水平面的动摩擦因数为多少?
(2)圆盘转动的角速度应为多大?
【答案】(1)0.4 (2)5kπ rad/s,其中k=1,2,3
【解析】
(1)物块离开O′点后做平抛运动,可以求出平抛运动的初速度,然后根据运动学公式求解加速度,根据牛顿第二定律求解动摩擦因数;
(2)根据平抛运动的时间为圆盘转动周期的整数倍进行求解即可;
(1)小球离开![]() 点后做平抛运动,若正好落在A点,则:
点后做平抛运动,若正好落在A点,则:![]() ,
,![]()
得到:![]()
则小球由P到![]() 点的过程中,由运动学公式
点的过程中,由运动学公式![]() 得:
得:![]()
由牛顿第二定律得:![]()
可以得到:![]() ;
;
(2)为了使小球刚好落在A点,则小球下落的时间为圆盘转动周期的整数倍,
即有:![]() ,其中
,其中![]()
即![]() ,其中
,其中![]() 。
。

练习册系列答案
相关题目
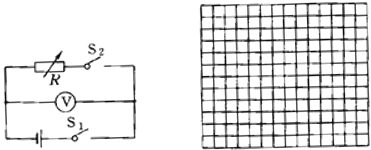
【题目】在测电源电动势和内阻的实验中,用电源、电阻箱、电压表连成如实验图所示电路.一位同学记录的6组数据见下表:
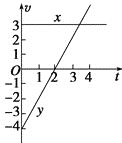
试根据这些数据在坐标纸上选择适当的坐标轴,并在实验图的方格纸上画出图线_____,根据图线读出电源的电动势E=____V,求得电源的内阻r=____Ω。
R/Ω | 2.0 | 3.0 | 6.0 | 10 | 15 | 20 |
U/V | 1.30 | 1.36 | 1.41 | 1.48 | 1.49 | 1.50 |