Question

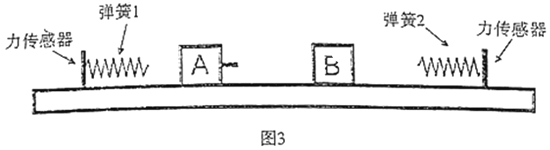
【题目】如图，光滑水平面上放置一质量为mA＝1kg的物体A，长L＝11m的传送带以v＝30m/s的速度顺时针匀速转动，物体A与传送带的动摩擦因数为μ＝0.8，传送带右侧光滑水平面上静止放置一物块B，B质量mB＝3kg。传送带与水平面之间的缝隙均可忽略。物体B用细线与光滑轨道上的小车C相连，细绳刚好处于伸直状态，小车的质量为mC＝4kg。现给A一个向右的水平速度V0＝20m/s，经过传送带后，A与B碰撞并立即黏连为一个整体，碰撞时间可忽略。当AB一起向右运动到最高点时，细绳突然断裂，细绳断裂后小车被挡板挡住，AB恰能沿光滑圆轨道切线方向滑入，圆轨道的末端恰在圆轨的最高点，其中入射点与圆心的连线和竖直方向的夹角为α＝53°，已知sin53°＝0.8，cos53°＝0.6，重力加速度g＝10m/s2．求：

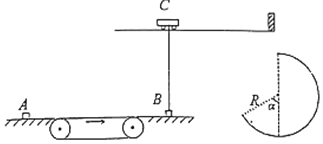
(1)A与B碰撞后整体的速度大小；

(2)AB上升到最高点的速度；

(3)要使AB在圆弧轨道上运动时不脱离圆弧，圆弧R满足的条件。

Answer 1

【答案】(1)6m/s(2)3m/s(3) 或

【解析】

(1)设A在传送带上一直做加速运动，A到达传送带的另一端的速度为v1，选取向右为正方向，则有：

代入数据可得：

v1＝24m/s＜v

可知A离开传送带的速度为24m/s，A与B碰撞的过程中水平方向的动量守恒，选取向右为正方向，则有：

mAv1＝(mA+mB)v2

代入数据可得：

v2＝6m/s

(2)AB与C一起向右运动的过程中水平方向的动量守恒，当AB到达最高点时，它们的速度是相等的，则有：

(mA+mB)v2＝(mA+mB+mC)v2

可得：

v3＝3m/s

(3)绳子断开后AB做平抛运动，切入圆轨道时：

代入数据可得：

v4＝4m/s

合速度为：

①当AB整体恰好到达与O等高处时，设圆的半径为R1，则有：

代入数据可得：

②当AB整体能通过最高点时，设在最高点的速度为v5，在最高点有：

从切入点到最高点的过程中机械能守恒，则有：

代入数据可得：

所以圆弧R满足

或