题目内容
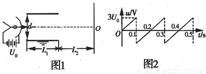
如图1所示,电子由阴极飞出时的初速度忽略不计,电子发射装置的加速电压为U.电容器板长为L1,板间距离为d,下极板接地.电容器右端到荧光屏的距离为L2.在电容器两极板间接一交变电压,上极板的电势随时间变化的图象如图2所示,每个电子穿过平行板的时间极短,可以认为电压是不变的.求:(1)电子打在荧光屏上的位置到O点的距离y与交变电压u的函数关系式;
(2)若L1=L2=d=10cm,则t=0.06s时刻,电子打在荧光屏上的位置距离O点的距离.
【答案】分析:(1)电子先经加速电场加速,根据动能定理得到速度的表达式;再进行偏转电场中做类平抛运动,运用运动的分解法,由牛顿第二定律和运动学公式推导出电子离开电场时偏转距离与u的关系;最后电子做匀速直线运动,由几何知识求y与u的关系式;
(2)由图2读出t=0.06s时刻的电压,将若L1=L2=d=10cm代入上题的结论,即可求解.
解答:解:(1)电子经加速电场加速,有qU=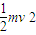
经偏转电场后侧向偏转的距离y′=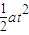 =
= ?
?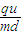
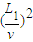
联立以上两式得:y′=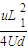
根据几何知识得: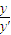 =
=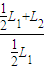
则得y=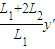 =
=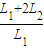 ?
?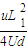 =
=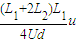
(2)由图2读出t=0.06s时刻的电压u=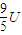 ,L1=L2=d=10cm,代入上式得y=
,L1=L2=d=10cm,代入上式得y=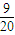 L1=4.5cm
L1=4.5cm
答:
(1)电子打在荧光屏上的位置到O点的距离y与交变电压u的函数关系式是y=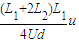 ;
;
(2)若L1=L2=d=10cm,则t=0.06s时刻,电子打在荧光屏上的位置距离O点的距离是4.5cm.
点评:本题是带电粒子在组合场中运动的类型,关键要分析电子的运动情况,对类平抛运动会进行分解,结合几何知识进行求解.
(2)由图2读出t=0.06s时刻的电压,将若L1=L2=d=10cm代入上题的结论,即可求解.
解答:解:(1)电子经加速电场加速,有qU=
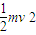
经偏转电场后侧向偏转的距离y′=
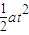 =
= ?
?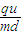
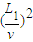
联立以上两式得:y′=
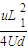
根据几何知识得:
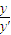 =
=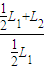
则得y=
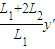 =
=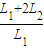 ?
?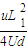 =
=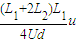
(2)由图2读出t=0.06s时刻的电压u=
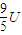 ,L1=L2=d=10cm,代入上式得y=
,L1=L2=d=10cm,代入上式得y=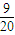 L1=4.5cm
L1=4.5cm答:
(1)电子打在荧光屏上的位置到O点的距离y与交变电压u的函数关系式是y=
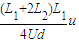 ;
;(2)若L1=L2=d=10cm,则t=0.06s时刻,电子打在荧光屏上的位置距离O点的距离是4.5cm.
点评:本题是带电粒子在组合场中运动的类型,关键要分析电子的运动情况,对类平抛运动会进行分解,结合几何知识进行求解.

练习册系列答案
相关题目
(1)如图所示,用某单色光照射光电管的阴板K,会发生光电效应.在阳极A和阴极K之间加上反向电压,通过调节滑动变阻器的滑片逐渐增大加在光电管上的电压,直至电流表中电流恰为零,此时电压表的电压值U称为反向截止电压,现分别用频率为 和
和 的单色光照射阴极,测得反向截止电压分别为U1和U2.设电子的质量为m、电荷量为e,,下列说法正确的是 .(选对1个给3分,选对2个给4分,选对3个给6分,每选错1个扣3分,最低得分为0分)
的单色光照射阴极,测得反向截止电压分别为U1和U2.设电子的质量为m、电荷量为e,,下列说法正确的是 .(选对1个给3分,选对2个给4分,选对3个给6分,每选错1个扣3分,最低得分为0分)
A.频率为 的光照射时,光电子的最大初速度为 的光照射时,光电子的最大初速度为 |
B.频率为 的光照射时,光电子的最大初速度为 的光照射时,光电子的最大初速度为 |
C.阴极K金属的逸出功为 |
D.普朗克常数 |

(2)如图所示,A、B两球质量均为m,其间有压缩的轻短弹簧处于锁定状态(A、B两球与弹簧两端接触但不连接).弹簧的长度、两球的大小均忽略,整体视为质点,该装置从半径为R的竖直光滑圆轨道左侧与圆心等高处由静止下滑,滑至最低点时,解除对弹簧的锁定状态之后,B球恰好能到达轨道最高点,求:

①小球B解除锁定后的速度
②弹簧处于锁定状态时的弹性势能
 和
和 的单色光照射阴极,测得反向截止电压分别为U1和U2.设电子的质量为m、电荷量为e,,下列说法正确的是 .(选对1个给3分,选对2个给4分,选对3个给6分,每选错1个扣3分,最低得分为0分)
的单色光照射阴极,测得反向截止电压分别为U1和U2.设电子的质量为m、电荷量为e,,下列说法正确的是 .(选对1个给3分,选对2个给4分,选对3个给6分,每选错1个扣3分,最低得分为0分)





