题目内容
如图所示，光滑导轨EF、GH等高平行放置，EG间宽度为FH间宽度的3倍，导轨右侧水平且处于竖直向上的匀强磁场中，左侧呈弧形升高。ab、cd是质量均为m的金属棒，现让ab从离水平轨道h高处由静止下滑，设导轨足够长。试求：
（1）ab、cd棒的最终速度。
（2）全过程中感应电流产生的焦耳热。
（1）ab自由下滑，机械能守恒：mgh=
mv2 [1]
由于ab、cd串联在同一电路中，任何时刻通过的电流总相等，金属棒有效长度Lab=3Lcd，故它们的磁场力为：Fab=3Fcd [2]
在磁场力作用下，ab、cd各做变速运动，产生的感应电动势方向相反，当Eab=Ecd时，电路中感应电流为零（I=0），安培力为零，ab、cd运动趋于稳定，此时有：BLabvab=BLcdvcd，所以vab=vcd/3 [3]
ab、cd受磁场力作用，动量均发生变化，由动量定理得：
FabΔt=m（v-vab）[4]
FcdΔt=mvcd[5]
联立以上各式解得：Vab=
，
Vcd=
（2）根据系统能量守恒可得：Q=ΔE机=mgh-
m（Vab2+Vcd2）=
mgh
练习册系列答案
相关题目
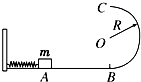如图所示，光滑水平面AB与竖直面内的光滑半圆形导轨在B点相接，导轨半径为R．一个质量为m的物体将弹簧压缩至A点后由静止释放，在弹力作用下物体获得某一向右速度后脱离弹簧，之后向上运动恰能完成半个圆周运动到达C点．试求：
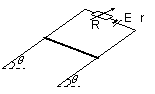
如图所示，光滑的平行导轨倾角为θ，处在磁感应强度为B的匀强磁场中，导轨中接入电动势为E、内阻为r的直流电源．电路中有一阻值为R的电阻，其余电阻不计，将质量为m、长为L的导体棒由静止释放，求导体棒在释放瞬间的加速度的大小．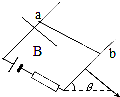
如图所示，光滑的平行导轨倾角为θ，处于垂直导轨平面磁感应强度为B的匀强磁场中，导轨中接入电动势为E．内阻为r的直流电源，电路中有一阻值为R的电阻，其余电阻不计，将质量为m．长度为L的导体棒由静止释放，求导体棒在释放瞬间的加速度的大小．
