题目内容
12.如图甲所示,水平直线MN上方有竖直向下的匀强电场,场强大小E=π×103 N/C,MN下方有垂直于纸面的磁场,磁感应强度B随时间t按如图乙所示规律做周期性变化,规定垂直纸面向外为磁场正方向.t=0时将一重力不计、比荷$\frac{q}{m}$=106C/kg的正点电荷从电场中的O点由静止释放,在t1=1×10-5s时恰通过MN上的P点进入磁场,P点左方d=124cm处有一垂直于MN且足够大的挡板.已知 sin53°=cos37°=0.8,sin37°=cos53°=0.6.求:
(1)电荷从P点进入磁场时速度的大小υ0;
(2)电荷在t2=8×10-5 s时与P点的距离△s;
(3)电荷从O点出发运动到挡板所需时间t总.
分析 (1)由牛顿第二定律结合运动学公式求出电荷进入磁场时的速度大小;
(2)结合粒子做圆周运动的周期与磁场交变周期的关系,作出电荷的运动轨迹,由几何知识求t2=8×10-5s时电荷与P点的距离;
(3)作出电荷最后d-s内的轨迹图,由几何关系确定其转过的圆心角,总时间为四个运动阶段的时间之和.
解答 解:(1)电荷在电场中做匀加速直线运动,则Eq=ma
又 υ0=at1
解得:υ0=$\frac{qE{t}_{1}}{m}$=π×103×106×1×10-5 m/s=π×104 m/s
(2)电荷在磁场中做匀速圆周运动,洛伦兹力提供向心力,有:qυB=m$\frac{{v}^{2}}{r}$,
得:r=$\frac{mυ}{Bq}$
当B1=$\frac{π}{20}$ T时,半径为:r1=$\frac{mυ0}{B1q}$=0.2 m=20 cm,求其中的一个半径即得
周期T1=$\frac{2πm}{B1q}$=4×10-5 s,求其中的一个周期即得.
当B2=$\frac{π}{30}$ T时,半径r2=$\frac{m{v}_{0}}{q{B}_{2}}$=0.3 m=30 cm
周期T2=$\frac{2πm}{q{B}_{2}}$=6×10-5 s
故电荷从t=0时刻开始做周期性运动,其运动轨迹如图所示.
在t=0到t2=8×10-5 s时间内,电荷先沿直线OP运动t1,再沿小圆轨迹运动$\frac{{T}_{1}}{4}$,紧接着沿大圆轨迹运动T2,t2=8×10-5 s时电荷与P点的距离△s=$\sqrt{2}$r1=20$\sqrt{2}$ cm
(3)电荷从P点开始的运动周期T=1×10-4 s,且在每一个T内向左沿PM移动s1=2r1=40 cm,电荷到达挡板前经历了完整周期数N=$\frac{d-{r}_{1}-{r}_{2}}{{s}_{1}}$+1=2.85,取N=2,则沿PM运动距离s=2s1=80 cm,设电荷撞击挡板前速度方向与水平方向成θ角,最后d-s=44 cm内的轨迹如图所示.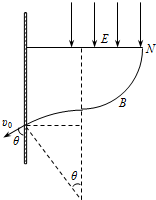
据几何关系有r1+r2sinθ=0.44
解得sinθ=0.8,即θ=53°
则电荷从O点出发运动到挡板所需总时间
t总=t1+2T+$\frac{{T}_{1}}{4}$+$\frac{θ}{360°}{T}_{2}$
解得t总=2.29×10-4 s
答:(1)电荷从P点进入磁场时速度的大小υ0是π×104 m/s.
(2)电荷在t2=8×10-5 s时与P点的距离△s是20$\sqrt{2}$ cm.
(3)电荷从O点出发运动到挡板所需时间t总是2.29×10-4 s.
点评 带电粒子在电场、磁场和重力场等共存的复合场中的运动,其受力情况和运动图景都比较复杂,但其本质是力学问题,应按力学的基本思路,运用力学的基本规律研究和解决此类问题.

 中考解读考点精练系列答案
中考解读考点精练系列答案| A. | 磁铁对磁铁 | B. | 通电直导线对静止的电荷 | ||
| C. | 电流对磁铁 | D. | 磁铁对电流 |
 如图所示,小球被细线悬挂于O点,若将小球拉至水平后由静止释放,不计阻力,已知小球在下摆过程中速度逐渐增大,则在小球下摆到最低点的过程中( )
如图所示,小球被细线悬挂于O点,若将小球拉至水平后由静止释放,不计阻力,已知小球在下摆过程中速度逐渐增大,则在小球下摆到最低点的过程中( )| A. | 重力对物体做正功 | B. | 绳拉力对小球做正功 | ||
| C. | 重力的功率先增大后减小 | D. | 重力平均功率为零 |
 如图所示,开关S闭合电灯不亮,为了检查电路故障,现用电压表进行测量,结果是UAE=2.5V,UBC=0,UDE=2.5V,则电路故障原因是( )
如图所示,开关S闭合电灯不亮,为了检查电路故障,现用电压表进行测量,结果是UAE=2.5V,UBC=0,UDE=2.5V,则电路故障原因是( )| A. | 电阻R断路 | B. | 电灯L断路 | C. | R、L同时电路 | D. | 变压器R′断路 |
| A. | P | B. | $\frac{{P}^{2}R}{{U}^{2}}$ | C. | $\frac{{U}^{2}}{R}$ | D. | P-$\frac{{P}^{2}R}{{U}^{2}}$ |
| A. | 气体从外界吸收热量,其内能必然增大 | |
| B. | 用外力压缩气体使其体积减小,其内能必然增大 | |
| C. | 若和外界没有热交换,在真空中自由膨胀的过程中,其内能必定减小 | |
| D. | 若温度升高,其内能必然增大 |