题目内容
(14分)如图,倾角为θ的斜面固定在水平地面上(斜面底端与水平地面平滑连接),A点位于斜面底端,AB段斜面光滑,长度为s,BC段足够长,物体与BC段斜面、地面间的动摩擦因数均为μ。质量为m的物体在水平外力F的作用下,从A点由静止开始沿斜面向上运动,当运动到B点时撤去力F。求:

(1)物体上滑到B点时的速度vB;
(2)物体最后停止时距离A点的距离。

(1)物体上滑到B点时的速度vB;
(2)物体最后停止时距离A点的距离。
(1)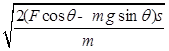 (2)若mgsinθ≤μmgcosθ时,物体最后停止时距离A点的距离
(2)若mgsinθ≤μmgcosθ时,物体最后停止时距离A点的距离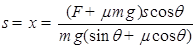 .若mgsinθ>μmgcosθ时,最后在水平面上滑行的距离为
.若mgsinθ>μmgcosθ时,最后在水平面上滑行的距离为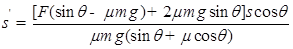
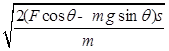 (2)若mgsinθ≤μmgcosθ时,物体最后停止时距离A点的距离
(2)若mgsinθ≤μmgcosθ时,物体最后停止时距离A点的距离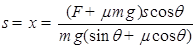 .若mgsinθ>μmgcosθ时,最后在水平面上滑行的距离为
.若mgsinθ>μmgcosθ时,最后在水平面上滑行的距离为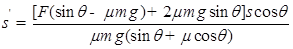
试题分析:(1)对于物体从A到B的过程,由动能定理得:

则得:
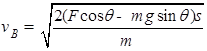
(2)设物体运动到最高点时距离A点的距离为x.对整个过程,由动能定理得:
Fscosθ-mgxsinθ-μmg(x-s)cosθ=0
解得:

若mgsinθ≤μmgcosθ时,物体最后停止时距离A点的距离
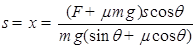 .
.若mgsinθ>μmgcosθ时,物体下滑,设最后在水平面上滑行的距离为S′.对全过程,由动能定理得:
Fs-2μmg(x-s)cosθ-μmgS′=0
则得:
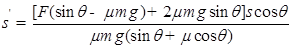

练习册系列答案
相关题目

 =L2,小物块与两个平面的动摩擦因数相同,由以上数据可以求出物体与平面间的动摩擦因数μ=________.
=L2,小物块与两个平面的动摩擦因数相同,由以上数据可以求出物体与平面间的动摩擦因数μ=________.





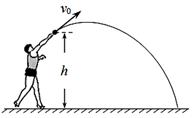
 为0.40,小车与水平面间的摩擦忽略不计,(取g=10m/s2),求:
为0.40,小车与水平面间的摩擦忽略不计,(取g=10m/s2),求:
 时,A物块上升的高度为L;若A、B不粘连,用一竖直向上的恒力
时,A物块上升的高度为L;若A、B不粘连,用一竖直向上的恒力 作用在B上,当A物块上升的高度也为L时,A、B恰好分离。求:
作用在B上,当A物块上升的高度也为L时,A、B恰好分离。求:
 ;
;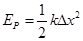 ,k为弹簧的劲度系数,Δx为弹簧的形变量)
,k为弹簧的劲度系数,Δx为弹簧的形变量)