题目内容
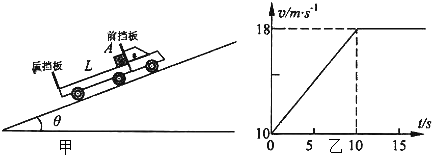
如图甲一辆货车在倾角θ=37°的足够长的斜坡上以速度v=10m/s匀速行驶,货车质量M=2×103kg、车厢长L=10.5m,车厢上表面粗糙.车厢内紧靠车厢前挡板处有一正方体物体A与货车相对静止一起运动,物体A边长10.5m,质量m=1×103kg,从t=0时刻货车开始加速,物体A与车厢发生相对滑动.货车开始加速后的v-t图象如图乙所示,物体A与车厢后挡板刚接触时恰好与货车速度相同.已知斜坡对货车阻力大小为货车对斜坡压力的0.1倍,空气阻力不计,sin37°=0.6,cos37°=0.8,g=10m/s2求:
(1)车厢与物体A间的动摩擦因数;
(2)物体A与车厢相对静止后,货车的输出功率.
(1)车厢与物体A间的动摩擦因数;
(2)物体A与车厢相对静止后,货车的输出功率.

分析:(1)对物体研究:由v-t图象看出,物体匀加速运动经过10s时间,根据速度图象可求得此过程物体通过的位移和末速度,再运用牛顿第二定律列式;对车:由平均速度公式可求得匀加速运动的距离,再根据两者位移关系列式,即可求解.
(2)物体A与车厢相对静止后,物体和车一起匀速运动,根据平衡条件求解牵引力,即可由P=Fv公式货车的输出功率.
(2)物体A与车厢相对静止后,物体和车一起匀速运动,根据平衡条件求解牵引力,即可由P=Fv公式货车的输出功率.
解答:解:(1)对物体m:根据牛顿第二定律得:
μmgcosθ-mgsinθ=mam,
通过的位移为 sm=v0t+
amt2
末速度为 vt=v0+amt,
对车:匀加速运动的距离:s1=
(v0+vt)t0=
×10=140m;
匀速运动车运动的距离为:s2=vt(t-t0)=18(t-10),
由几何关系得:L-l=(s1+s2)-sm,
由以上各式可得:μ=0.83;
(2)物体A与车厢相对静止后,物体与车一起以vm=18m/s速度匀速运动,则有:
根据平衡条件得:
牵引力 F=k(M+m)gcosθ+(M+m)gsinθ;
货车的输出功率为 P=Fvm.
由以上各式得:P=3.67×105W;
答:
(1)车厢与物体A间的动摩擦因数是0.83;
(2)物体A与车厢相对静止后,货车的输出功率为3.67×105W.
μmgcosθ-mgsinθ=mam,
通过的位移为 sm=v0t+
| 1 |
| 2 |
末速度为 vt=v0+amt,
对车:匀加速运动的距离:s1=
| 1 |
| 2 |
| 10+18 |
| 2 |
匀速运动车运动的距离为:s2=vt(t-t0)=18(t-10),
由几何关系得:L-l=(s1+s2)-sm,
由以上各式可得:μ=0.83;
(2)物体A与车厢相对静止后,物体与车一起以vm=18m/s速度匀速运动,则有:
根据平衡条件得:
牵引力 F=k(M+m)gcosθ+(M+m)gsinθ;
货车的输出功率为 P=Fvm.
由以上各式得:P=3.67×105W;
答:
(1)车厢与物体A间的动摩擦因数是0.83;
(2)物体A与车厢相对静止后,货车的输出功率为3.67×105W.
点评:解答本题首先要明确物体和车的运动情况,结合图象的物理意义,求解相关的位移,其次关键是寻找两者位移之间的关系.

练习册系列答案
相关题目
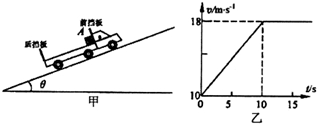








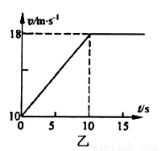
 (3)摩擦力对物体A所做的功。
(3)摩擦力对物体A所做的功。