Question

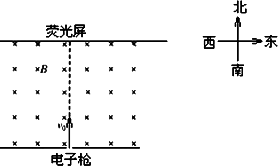
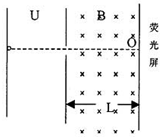在电子显像管内部，由炽热的灯丝上发射出的电子在经过一定的电压加速后，进入偏转磁场区域，最后打到荧光屏上，当所加的偏转磁场的磁感强度为零时，电子应沿直线运动打在荧光屏的正中心位置．但由于地磁场对带电粒子运动的影响，会出现在未加偏转磁场时电子束偏离直线运动的现象，所以在精密测量仪器的显像管中常需要在显像管的外部采取磁屏蔽措施以消除地磁场对电子运动的影响．已知电子质量为m、电荷量为e，从炽热灯丝发射出的电子（可视为初速度为零）经过电压为U的电场加速后，沿水平方向由南向北运动．若不采取磁屏蔽措施，且已知地磁场磁感强度的竖直向下分量的大小为B，地磁场对电子在加速度过程中的影响可忽略不计．在未加偏转磁场的情况下，求：
（1）电子束将偏向什么方向；
（2）电子在磁场中运动的半径；
（3）若加速电场边缘到荧光屏的距离为L，求在磁场的作用下打到荧光屏的电子与0点的距离．

Answer 1

分析：（1）电子在地磁场中受到洛伦兹力作用，根据左手定则判断出洛伦兹力的方向，即可知道电子束的偏转方向；
（2）根据洛伦兹力等于向心力，列式求出电子在磁场中运动的半径；
（3）画出轨迹，根据几何知识求解打到荧光屏的电子与0点的距离．

解答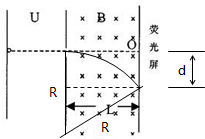： 解：（1）根据左手定则可以判断出电子束将偏向东方．
（2）设从加速电场射出的电子速度为v₀，则根据动能定理有：

1

2

m

v

2 0

=eU
从加速电场射出的电子在地磁场中受到洛伦兹力的作用而做匀速圆周运动，设电子在地磁场中运动的半径为RR，根据牛顿第二定律得
  ev₀B=m

v 2 0

R

由以上各式解得  R=

mv0

eB

=

1

B

2mU e

（3）设电子在荧光屏上偏移的距离为x根据图中的几何关系，有：d=R-

R2-L2

结合以上关系得d=

1

B

2mU e

-

2mU eB2 -L2

答：
（1）电子束将向东偏．
（2）电子在磁场中运动的半径是

1

B

2mU e

．
（3）在磁场的作用下打到荧光屏的电子与0点的距离是得

1

B

2mU e

-

2mU eB2 -L2

．

点评：本题是带电粒子在磁场中匀速圆周运动的问题，掌握左手定则、画出轨迹，运用几何知识是解题的关键．