题目内容
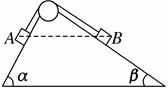
如图所示,两个内壁光滑、半径不同的半球形碗放在不同高度的水平面上,使两碗口处于同一水平面,现将质量相同的两个小球(小球半径远小于碗的半径),分别从两个碗的边缘由静止释放,当两球分别通过碗的最低点时( )
| A.两球的速度大小相等 |
| B.两球的机械能大小始终相等 |
| C.两球对碗底的压力大小相等 |
| D.小球下滑的过程中重力的功率先增大后减小 |
BCD
解析试题分析:小球在运动过程中受重力mg和碗的支持力N作用,且支持力N始终不做功,根据动能定理有:mgR=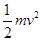 -0,解得小球通过碗的最低点时的速度大小为:v=
-0,解得小球通过碗的最低点时的速度大小为:v=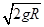 ,由于两碗的半径不等,因此两球通过碗的最低点时的速度大小不相等,故选项A错误;整个运动过程中机械能守恒,由于初始时两球质量相等、高度相等,且均由静止释放,因此整个过程中,两球的机械能大小始终相等,故选项B正确;在碗的最低点处,根据牛顿第二定律有:N-mg=
,由于两碗的半径不等,因此两球通过碗的最低点时的速度大小不相等,故选项A错误;整个运动过程中机械能守恒,由于初始时两球质量相等、高度相等,且均由静止释放,因此整个过程中,两球的机械能大小始终相等,故选项B正确;在碗的最低点处,根据牛顿第二定律有:N-mg=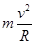 ,解得:N=3mg,与碗的半径无关,故选项C正确;根据瞬时功率的计算公式可知,小球下滑的过程中重力的功率为:P=mgvcosα,释放时v=0,通过最低点时cosα=0,而在中间某一位置处mgvcosα≠0,所以小球下滑的过程中重力的功率先增大后减小,故选项D正确。
,解得:N=3mg,与碗的半径无关,故选项C正确;根据瞬时功率的计算公式可知,小球下滑的过程中重力的功率为:P=mgvcosα,释放时v=0,通过最低点时cosα=0,而在中间某一位置处mgvcosα≠0,所以小球下滑的过程中重力的功率先增大后减小,故选项D正确。
考点:本题主要考查了瞬时功率计算公式、动能定理、机械能守恒定律、牛顿第二定律的应用问题,属于中档题。

 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案如图所示为某中学科技小组制作的利用太阳能驱动小车的装置.当太阳光照射到小车上方的光电板时,光电板中产生的电流经电动机带动小车前进.若质量为m的小车在平直的水泥路上从静止开始沿直线加速行驶,经过时间t前进的距离为s,且速度达到最大值vm.设这一过程中电动机的功率恒为P,小车所受阻力恒为F,那么这段时间内 
| A.小车做匀加速运动 |
| B.小车受到的牵引力逐渐增大 |
| C.小车受到的合外力所做的功为Pt |
D.小车受到的牵引力做的功为Fs+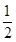 mv mv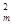 |
如图所示,滑块以速率v1沿斜面由底端向上滑行,至某一位置后返回,回到出发点时的速率变为v2,且v2<v1,则下列说法中错误的是
| A.全过程中重力做功为零 |
| B.在上滑和下滑两过程中,机械能减少 |
| C.在上滑和下滑两过程中,摩擦力做功相等 |
| D.在上滑和下滑两过程中,摩擦力的平均功率相等 |
如图所示,两个质量不同的物体A和B,分别从两个相同高度光滑斜面和光滑圆弧斜坡的顶点,从静止开始下滑到底部,下列说法正确的是
| A.它们到达底部时的速度大小相等 |
| B.下滑过程中重力做的功相等 |
| C.它们在顶点时的机械能相等 |
| D.它们到达底部时的动能相等 |
如图所示,一恒力F与水平方向夹角为θ,作用在置于光滑水平面、质量为m的物体上,作用时间为t,沿水平面运动的位移为s,则( )
| A.F的冲量大小为Ftcosθ |
| B.F的冲量大小为Ft |
| C.F做功大小为Fs |
| D.F做功大小为Fscosθ |
用恒力F使质量M的物体沿竖直匀速上升h,恒力做功W1,再用该恒力作用于质量m(m<M)的物体,使之在竖直方向加速上升距离h,恒力做功W2,则两次恒力做功的关系是
| A.W1=W2 | B.W1<W2 | C.W1>W2 | D.无法判断 |
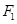 、
、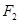 、
、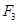 将质量为
将质量为 的物体由静止沿同一光滑斜面以相同的加速度从斜面底端拉到斜面的顶端,在此过程中,
的物体由静止沿同一光滑斜面以相同的加速度从斜面底端拉到斜面的顶端,在此过程中,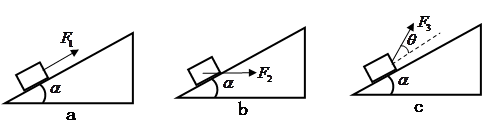
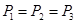


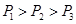
 图象(图中AB、BC均为直线且BC延长线交于O点),假设电动车行驶中所受的阻力恒定,则 ( )
图象(图中AB、BC均为直线且BC延长线交于O点),假设电动车行驶中所受的阻力恒定,则 ( )