题目内容
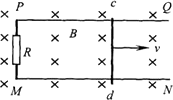
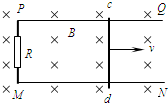
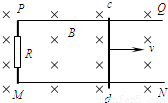
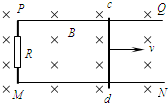 空间某区域存在水平方向的匀强磁场,磁感应强度B=1.0T.在磁场区域内有两根相距L=0.80m的平行金属导轨PQ、MN,固定在竖直平面内,如图所示.PM间连接有R=3.0Ω的电阻.导体棒cd沿导轨平面向右匀速运动,在回路中产生的电流I=0.60A.求:
空间某区域存在水平方向的匀强磁场,磁感应强度B=1.0T.在磁场区域内有两根相距L=0.80m的平行金属导轨PQ、MN,固定在竖直平面内,如图所示.PM间连接有R=3.0Ω的电阻.导体棒cd沿导轨平面向右匀速运动,在回路中产生的电流I=0.60A.求:(1)导体棒cd所受安培力F的大小;
(2)t=2.0s时间内电流在电阻R上产生的焦耳热.
分析:(1)由E=BLv求出导体棒切割磁感线产生的感应电动势,由欧姆定律求出感应电流;由F=BIL求出导体棒受到的安培力;
(2)由焦耳定律求出导体棒匀速运动时产生的焦耳热.
(2)由焦耳定律求出导体棒匀速运动时产生的焦耳热.
解答:解:
(1)导体棒cd所受安培力的大小F=BIL=1.0×0.6×0.8N=0.48N
(2)t=2.0s时间内电流在电阻R上产生的焦耳热Q=I2Rt=0.62×3.0×2.0J=2.16J
答:(1)导体棒cd所受安培力F的大小是0.48N;
(2)t=2.0s时间内电流在电阻R上产生的焦耳热是2.16J.
(1)导体棒cd所受安培力的大小F=BIL=1.0×0.6×0.8N=0.48N
(2)t=2.0s时间内电流在电阻R上产生的焦耳热Q=I2Rt=0.62×3.0×2.0J=2.16J
答:(1)导体棒cd所受安培力F的大小是0.48N;
(2)t=2.0s时间内电流在电阻R上产生的焦耳热是2.16J.
点评:本题考查电磁感应定律的应用,难度不大,熟练应用基础知识即可正确解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
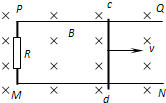 如图所示,空间某区域存在水平方向的匀强磁场,磁感应强度B=1.0T.在磁场区域内有两根相距L=0.50m的平行金属导轨PQ、MN固定在竖直平面内,PM间连接有R=5.0Ω的电阻.当导体棒cd沿导轨平面向右匀速运动时,在闭合回路中产生的电流I=0.20A.求:
如图所示,空间某区域存在水平方向的匀强磁场,磁感应强度B=1.0T.在磁场区域内有两根相距L=0.50m的平行金属导轨PQ、MN固定在竖直平面内,PM间连接有R=5.0Ω的电阻.当导体棒cd沿导轨平面向右匀速运动时,在闭合回路中产生的电流I=0.20A.求: