题目内容
2.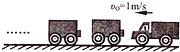 某辆货车以v0=1m/s的速度驶向停在水平道路上的9节挂车,与它们对接,设货车和挂车的质量都相等,水平道路的摩擦忽略不计.货车与笫一节挂车相碰后,它们连在一起具有一个相同的速度是0.5m/s;紧接着又与第二节挂车相碰,就这样直至碰上最后一节挂车,与最后一节碰撞后,整体的速度0.1m/s.
某辆货车以v0=1m/s的速度驶向停在水平道路上的9节挂车,与它们对接,设货车和挂车的质量都相等,水平道路的摩擦忽略不计.货车与笫一节挂车相碰后,它们连在一起具有一个相同的速度是0.5m/s;紧接着又与第二节挂车相碰,就这样直至碰上最后一节挂车,与最后一节碰撞后,整体的速度0.1m/s.
分析 货车与挂车碰撞过程系统动量守恒,货车与第一节挂车碰撞过程货车与第一节挂车系统动量守恒,由动量守恒定律可以求出碰撞后的速度;以货车与9节挂车组成的系统我研究对象,由动量守恒定律可以求出整体的速度.
解答 解:货车与挂车碰撞连接过程系统动量守恒,以货车的初速度方向为正方向,
货车与第一节挂车碰撞过程,由动量守恒定律得:mv0=(m+m)v1,解得:v1=0.5m/s,
以货车与9节挂车组成的系统为研究对象,由动量守恒定律得:mv0=(m+9m)v,解得:v=0.1m/s;
故答案为:0.5;0.1.
点评 本题考查了求速度,考查了动量守恒定律的应用,货车与挂车连接过程系统动量守恒,应用动量守恒定律可以解题,解题时要注意所选择研究对象的质量是多少.

练习册系列答案
相关题目
13.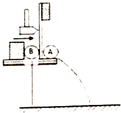 如图实验中,用小锤打击金属片后,A球水平抛出,B球自由下落,它们落至同一水平地面的过程中,所受重力做的功分别为WA、WB,重力的功率分别为PA、PB,不计空气阻力,则( )
如图实验中,用小锤打击金属片后,A球水平抛出,B球自由下落,它们落至同一水平地面的过程中,所受重力做的功分别为WA、WB,重力的功率分别为PA、PB,不计空气阻力,则( )
 如图实验中,用小锤打击金属片后,A球水平抛出,B球自由下落,它们落至同一水平地面的过程中,所受重力做的功分别为WA、WB,重力的功率分别为PA、PB,不计空气阻力,则( )
如图实验中,用小锤打击金属片后,A球水平抛出,B球自由下落,它们落至同一水平地面的过程中,所受重力做的功分别为WA、WB,重力的功率分别为PA、PB,不计空气阻力,则( )| A. | WA=WB,PA≠PB | B. | WA≠WB,PA=PB | C. | WA≠WB,PA≠PB | D. | WA=WB,PA=PB |
7. 如图为某台球室悬挂的吊灯,已知吊灯的质量为m,吊灯到地面的竖直距离为h1,到天花板的竖直距离为h2,小亮认为吊灯的重力势能为-mgh2,则他选择的参考平面为( )
如图为某台球室悬挂的吊灯,已知吊灯的质量为m,吊灯到地面的竖直距离为h1,到天花板的竖直距离为h2,小亮认为吊灯的重力势能为-mgh2,则他选择的参考平面为( )
 如图为某台球室悬挂的吊灯,已知吊灯的质量为m,吊灯到地面的竖直距离为h1,到天花板的竖直距离为h2,小亮认为吊灯的重力势能为-mgh2,则他选择的参考平面为( )
如图为某台球室悬挂的吊灯,已知吊灯的质量为m,吊灯到地面的竖直距离为h1,到天花板的竖直距离为h2,小亮认为吊灯的重力势能为-mgh2,则他选择的参考平面为( )| A. | 地面 | B. | 天花板 | ||
| C. | 台球桌的桌面 | D. | 吊灯所在的水平面 |
11.小球由地面竖直上抛,上升的最大高度为H,地面为零势能面,在上升至离地高度h处,小球的势能是动能的2倍,空气阻力不计,则h等于( )
| A. | $\frac{H}{4}$ | B. | $\frac{H}{3}$ | C. | $\frac{H}{2}$ | D. | $\frac{2H}{3}$ |
12.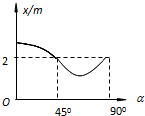 某研究性学习小组为了测量木块与木板间的动摩擦因数,让木块以一定的初速度v0沿倾角可在0~90°任意调整的木板向上滑行,测出木块沿木板向上所能达到的最大位移x,画出木块向上所能达到的最大位移x与对应木板倾角α的图象,如图所示,由该图可求得木块与木板间的动摩擦因数为(g取10m/s2)( )
某研究性学习小组为了测量木块与木板间的动摩擦因数,让木块以一定的初速度v0沿倾角可在0~90°任意调整的木板向上滑行,测出木块沿木板向上所能达到的最大位移x,画出木块向上所能达到的最大位移x与对应木板倾角α的图象,如图所示,由该图可求得木块与木板间的动摩擦因数为(g取10m/s2)( )
 某研究性学习小组为了测量木块与木板间的动摩擦因数,让木块以一定的初速度v0沿倾角可在0~90°任意调整的木板向上滑行,测出木块沿木板向上所能达到的最大位移x,画出木块向上所能达到的最大位移x与对应木板倾角α的图象,如图所示,由该图可求得木块与木板间的动摩擦因数为(g取10m/s2)( )
某研究性学习小组为了测量木块与木板间的动摩擦因数,让木块以一定的初速度v0沿倾角可在0~90°任意调整的木板向上滑行,测出木块沿木板向上所能达到的最大位移x,画出木块向上所能达到的最大位移x与对应木板倾角α的图象,如图所示,由该图可求得木块与木板间的动摩擦因数为(g取10m/s2)( )| A. | $\sqrt{2}$-1 | B. | 2-$\sqrt{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
 如图所示,轻质弹簧的自然长度为L0,劲度系数为k,现用水平推力缓慢地推弹簧,使弹簧缩短△x,求推力做的功,以及弹簧弹性势能的增加量.
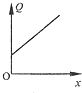
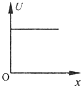
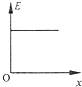
如图所示,轻质弹簧的自然长度为L0,劲度系数为k,现用水平推力缓慢地推弹簧,使弹簧缩短△x,求推力做的功,以及弹簧弹性势能的增加量.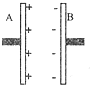 如图所示,一平行板电容器充电后与电源断开.以C表示电容器的电容、Q表示电容器所带电量、U表示两极板间的电压、E表示两板间的场强,若正极板保持不动,将负极板缓慢向右平移一小段距离的过程中,各物理量与负极板移动距离x的关系图象中正确的是( )
如图所示,一平行板电容器充电后与电源断开.以C表示电容器的电容、Q表示电容器所带电量、U表示两极板间的电压、E表示两板间的场强,若正极板保持不动,将负极板缓慢向右平移一小段距离的过程中,各物理量与负极板移动距离x的关系图象中正确的是( )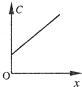
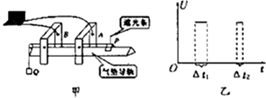 某学习小组利用气垫导轨验证机械能守恒定律,实验装置如图甲所示.当气垫导轨正常工作时导轨两侧喷出的气体使滑块悬浮在导轨上方,滑块与导轨间的阻力可忽略不计.在气垫导轨上相隔一定距离的两处安装两个光电传感器A、B,滑块P上固定一遮光条,若光线被遮光条遮挡,光电传感器会输出高电压,两光电传感器采集数据后与计算机相连.滑块在细线的牵引下向左加速运动,遮光条经过光电传感器A、B时,通过计算机可以得到如图乙所示的电压U随时间t变化的图线.
某学习小组利用气垫导轨验证机械能守恒定律,实验装置如图甲所示.当气垫导轨正常工作时导轨两侧喷出的气体使滑块悬浮在导轨上方,滑块与导轨间的阻力可忽略不计.在气垫导轨上相隔一定距离的两处安装两个光电传感器A、B,滑块P上固定一遮光条,若光线被遮光条遮挡,光电传感器会输出高电压,两光电传感器采集数据后与计算机相连.滑块在细线的牵引下向左加速运动,遮光条经过光电传感器A、B时,通过计算机可以得到如图乙所示的电压U随时间t变化的图线.